早教吧作业答案频道 -->数学-->
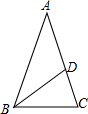
如图,在△ABC中,AB=AC=1,BC=5-12,在AC边上截取AD=BC,连接BD.(1)通过计算,判断AD2与AC•CD的大小关系;(2)求∠ABD的度数.
题目详情
如图,在△ABC中,AB=AC=1,BC=
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC•CD的大小关系;
(2)求∠ABD的度数.
| ||
| 2 |

(1)通过计算,判断AD2与AC•CD的大小关系;
(2)求∠ABD的度数.
▼优质解答
答案和解析
(1)∵AD=BC,BC=
,
∴AD=
,DC=1-
=
.
∴AD2=
=
,AC•CD=1×
=
.
∴AD2=AC•CD.
(2)∵AD=BC,AD2=AC•CD,
∴BC2=AC•CD,即
=
.
又∵∠C=∠C,
∴△BCD∽△ACB.
∴
=
=1,∠DBC=∠A.
∴DB=CB=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.
∵∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°.
解得:x=36°.
∴∠ABD=36°.
| ||
| 2 |
∴AD=
| ||
| 2 |
| ||
| 2 |
3-
| ||
| 2 |
∴AD2=
5+1-2
| ||
| 4 |
3-
| ||
| 2 |
3-
| ||
| 2 |
3-
| ||
| 2 |
∴AD2=AC•CD.
(2)∵AD=BC,AD2=AC•CD,
∴BC2=AC•CD,即
| BC |
| AC |
| CD |
| BC |
又∵∠C=∠C,
∴△BCD∽△ACB.
∴
| AB |
| AC |
| BD |
| CB |
∴DB=CB=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.
∵∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°.
解得:x=36°.
∴∠ABD=36°.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
读东西半球图,完成下列要求.(1)写出下图中字母所代表的大洲的名称:A,B.(2)A、B大洲的分界 2020-04-24 …
某凸透镜的焦距为10厘米,当物体沿主光轴从距透镜30厘米处向15厘米处移动时,则A像变大,像距变大 2020-05-16 …
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
A.πA,D(σC=D(R×S))B.πA,R,D(σS,C=R,D/(R×S))C.πA,R,D( 2020-05-26 …
A.πA,D(σC=D(R×S))B.πA,R.D(σR.C=S.D(R×S))C.πA,R.D(σ 2020-05-26 …
A、B、C、D均为中学化学常见的纯净物,A是单质.它们之间有如图所示的反应关系:(1)若B是气态氢 2020-06-17 …
求光栅常数d一束具有两种波长a和d的平行光垂直照射到一衍射光栅上,测得波长a的第三极主极大衍射角和 2020-07-10 …
已知A、B、C、D、A+C、B+C、A+D、B+D分别表示1到8这8个自然数,且互不相等,如果A是 2020-07-14 …
五个数a,b,c,d,e且a大于b,b大于c,c大于d,d大于e,它们两两和分别是183,186, 2020-07-23 …
一只蚂蚁从正方体一个顶点A沿表面,要爬到点C的最短距离为x,正方体棱长为a,正方体每个面的对角线长 2020-08-02 …