早教吧作业答案频道 -->数学-->
平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.(1)求证:四边形BFDE是矩形;(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
题目详情
平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
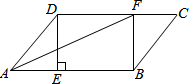
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.

(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
▼优质解答
答案和解析
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴DF∥BE,
∵CF=AE,
∴DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是平行四边形.
(2)∵AB∥CD,
∴∠BAF=∠AFD,
∵AF平分∠BAD,
∴∠DAF=∠AFD,
∴AD=DF,
在Rt△ADE中,∵AE=3,DE=4,
∴AD=
=5,
∴矩形的面积为20.
∴AB=CD,AB∥CD,
∴DF∥BE,
∵CF=AE,
∴DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是平行四边形.
(2)∵AB∥CD,
∴∠BAF=∠AFD,
∵AF平分∠BAD,
∴∠DAF=∠AFD,
∴AD=DF,
在Rt△ADE中,∵AE=3,DE=4,
∴AD=
| 32+42 |
∴矩形的面积为20.
看了 平行四边形ABCD中,过点D...的网友还看了以下:
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
A乘以B表示矩形,A除以B表示什么图形注意是表示的什么图形,例如三角形等,最好解释清楚A乘以B表示 2020-04-09 …
对于任意一个矩形A,令另一个矩形B的周长和面积分别是矩形A周长和面积的2倍(1)当矩形A的边长分别 2020-05-13 …
正方形A矩形B圆C的面积均为628其中矩形B的长是宽的2倍试比较他们的周长LaLbLc的大小解完本 2020-05-21 …
已知正方形A,矩形B,圆形C的面积均为628cm的平方,其中矩形B的长是宽的2倍,如果派取3.14 2020-07-27 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
下列判断正确的是()A.有一个角是直角的四边形是矩形B.有一组邻边相等的四边形是菱形C.有三个角是 2020-07-30 …
(2012•玉林)如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上, 2020-08-02 …
矩形是轴对称图形,下列说发正确的是A矩形有两条对称轴,这两条对称轴是它的对角线B矩形有一条对称轴, 2020-08-03 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …