早教吧作业答案频道 -->数学-->
在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F.(1)求证:△ABD是等边三角形;(2)求证:BE=AF.
题目详情
在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F.
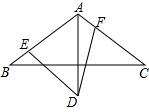
(1)求证:△ABD是等边三角形;
(2)求证:BE=AF.

(1)求证:△ABD是等边三角形;
(2)求证:BE=AF.
▼优质解答
答案和解析
(1)证明:连接BD,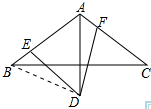
∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=
∠BAC,
∵∠BAC=120°,
∴∠BAD=∠DAC=
×120°=60°,
∵AD=AB,
∴△ABD是等边三角形;
(2)证明:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD
∵∠EDF=60°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
,
∴△BDE≌△ADF(ASA),
∴BE=AF.

∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=
| 1 |
| 2 |
∵∠BAC=120°,
∴∠BAD=∠DAC=
| 1 |
| 2 |
∵AD=AB,
∴△ABD是等边三角形;
(2)证明:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD
∵∠EDF=60°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
|
∴△BDE≌△ADF(ASA),
∴BE=AF.
看了 在△ABC中,AB=AC,∠...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
几何题,求证:D,A,E三点共线.在△ABC的BC边上任取一点P,作PD∥AC,PE∥AB,PD、 2020-06-04 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
矩阵平方差设方阵A满足A²-A-2E=O,求A的逆矩阵.答案是1/2(A-E).为啥不是1/2E, 2020-07-18 …
A,B均为三阶可逆矩阵,且A^3=0,则A:E-A,E+A均不可逆?B:E-A不可逆但E+A可逆? 2020-07-20 …
线性代数矩阵A满足A*=A^T,如a11,a12,a13为三个相等的正数,则a11为多少?由AA* 2020-07-25 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …
有AB二种元素,已知A元素原子的核电荷数为a,A的三负与B的N正的电子排布相同,则B原子的核电荷数为 2021-01-14 …