如图，抛物线y=ax2-2ax-3a交x轴于点A、B（A左B右），交y轴于点C，S△ABC=6，点P为第一象限内抛物线上的一点．（1）求抛物线的解析式；（2）若∠PCB=45°，求点P的坐标；（3）点Q为第四象限内抛

Question

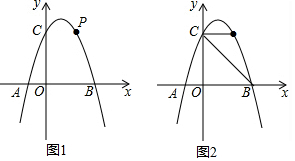
如图，抛物线y=ax²-2ax-3a交x轴于点A、B（A左B右），交y轴于点C，S_△ABC=6，点P为第一象限内抛物线上的一点．
（1）求抛物线的解析式；
（2）若∠PCB=45°，求点P的坐标；
（3）点Q为第四象限内抛物线上一点，点Q的横坐标比点P的横坐标大1，连接PC、AQ，当PC=(5)/(9)AQ时，求点P的坐标以及△PCQ的面积．

Answer 1

（1）∵抛物线y=ax²-2ax-3a=a（x+1）（x-3），
∴A（-1，0），B（3，0），C（0，-3a），
∴AB=4，OC=|-3a|=|3a|，
∵S_△ABC=6，
∴(1)/(2)AB•OC=6，
∴(1)/(2)×4×|3a|=6，
∴a=-1或a=1（舍），
∴抛物线的解析式为y=-x²+2x+3；
（2）由（1）知，B（3，0），C（0，-3a），
∴C（0，3），
∴OB=3，OC=3，
∴△OBC是等腰直角三角形，
∴∠BCO=∠OBC=45°，
∵点P为第一象限内抛物线上的一点，且∠PCB=45°，
∴PC∥OB，
∴P点的纵坐标为3，
由（1）知，抛物线的解析式为y=-x²+2x+3，
令y=3，∴-x²+2x+3=3，
∴x=0（舍）或x=2，
∴P（2，3）；
（3）如图2，过点P作PD⊥x轴交CQ于D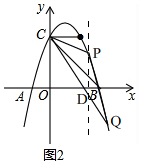，设P（3-m，-m²+4m）（0<m<1）；
∵C（0，3），
∴PC²=（3-m）²+（-m²+4m-3）²=（m-3）²[（m-1）²+1]，
∵点Q的横坐标比点P的横坐标大1，
∴Q（4-m，-m²+6m-5），
∵A（-1，0）．
∴AQ²=（4-m+1）²+（-m²+6m-5）²=（m-5）²[（m-1）²+1]
∵PC=(5)/(9)AQ，
∴81PC²=25AQ²，
∴81（m-3）²[（m-1）²+1]=25（m-5）²[（m-1）²+1]，
∵0<m<1，
∴[（m-1）²+1]≠0，
∴81（m-3）²=25（m-5）²，
∴9（m-3）=±5（m-5），
∴m=(1)/(2)或m=(26)/(7)（舍），
∴P（(5)/(2)，(7)/(4)），Q（(7)/(2)，-(9)/(4)），
∵C（0，3），
∴直线CQ的解析式为y=-(3)/(2)x+3，
∵P（(5)/(2)，(7)/(4)），
∴D（(5)/(2)，-(3)/(4)），
∴PD=(7)/(4)+(3)/(4)=(5)/(2)，
∴S_△PCQ=S_△PCD+S_△PQD=(1)/(2)PD×x_P+(1)/(2)PD×（x_Q-x_P）=(1)/(2)PD×x_Q=(1)/(2)×(5)/(2)×(7)/(2)=(35)/(8)．