早教吧作业答案频道 -->数学-->
如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.(3)如图
题目详情
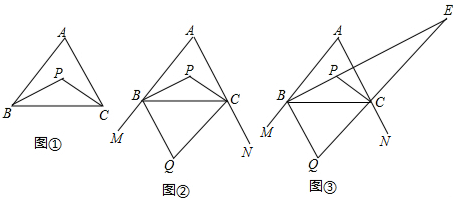
如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.

▼优质解答
答案和解析
(1) ∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°-
(∠ABC+∠ACB)=180°-
×100°=130°,
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=
(∠MBC+∠NCB)
=
(360°-∠ABC-∠ACB)
=
(180°+∠A)
=90°+
∠A
∴∠Q=90°-
∠A;
(3)∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,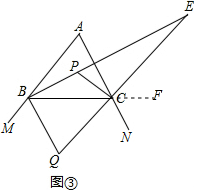
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=
∠A;
∵∠EBQ=∠EBC+∠CBQ
=
∠ABC+
∠MBC
=
(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°-
∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则
∠A=2(90°-
∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°-
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
∴∠Q=90°-
| 1 |
| 2 |
(3)∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,

∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=
| 1 |
| 2 |
∵∠EBQ=∠EBC+∠CBQ
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°-
| 1 |
| 2 |
④∠E=2∠Q,则
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,∠A的度数是90°或60°或120°.
看了 如图①,在△ABC中,∠AB...的网友还看了以下:
大多数概念间存在如图三种关系:下列概念间关系判断正确的是()概念I概念II相互关系A无机酸离子化合 2020-05-02 …
(2011•南京一模)对下列各曲线生物学含义的描述合理的是()A.如图表示人肌肉细胞中ATP生成速 2020-05-15 …
如图用圆的大小表示天体系统层次由高到低,与图示对应的天体系统是()A、河外星系、银河系、太阳系B、 2020-05-16 …
如图中圆的大小表示天体系统层次由高到低,下列天体系统与图示对应的分别是()A.河外星系、银河系、太 2020-05-16 …
假定有三个关系,学生关系S、课程关系C和学生选课关系SC,它们的结构如下:S(S#,SN,Sex,A 2020-05-26 …
一元二次根与系数的关系ax2+bx+c=0(a≠0)a,b,c的值与x1,x2的关系(例如:a,b 2020-06-09 …
红、黄、绿、蓝四个圈的周长(单位:厘米)分别用a、b、c、d表示,它们的关系如下:a÷b=b÷c= 2020-07-22 …
在15mL0.1mol·L-1KOH溶液中逐滴如入0.2mol·L-1甲酸溶液,溶液pH和加入的甲 2020-07-24 …
下列分析中正确的是()A.图中吸盘能将物体挂在墙上不掉下来,是因为重力与大气压力彼此平衡B.如图所示 2020-11-05 …
如图所示,设某热力学系统经历一个由c→d→e的过程,其中,ab是一条绝热曲线,a、c在如图所示,设某 2020-11-15 …