早教吧作业答案频道 -->数学-->
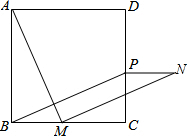
如图,在正方形ABCD中,点M是BC边上的任意一点,连接AM,并将线段AM绕点M顺时针旋转90°得到线段MN,过N作NP⊥CD于点P,连接BP.求证:四边形BMNP是平行四边形.
题目详情
如图,在正方形ABCD中,点M是BC边上的任意一点,连接AM,并将线段AM绕点M顺时针旋转90°得到线段MN,过N作NP⊥CD于点P,连接BP.求证:四边形BMNP是平行四边形.

▼优质解答
答案和解析
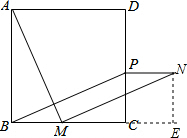 证明:过点N作NE⊥BC延长线于点E,
证明:过点N作NE⊥BC延长线于点E,
∵∠AMN=90°,
∴∠AMB+∠EMN=90°,
∵∠BAM+∠BMA=90°,
∴∠BAM=∠NME,
在△ABM和△MEN中,
,
∴△ABM≌△MEN(AAS),
∴AB=ME=BC,
则BM=EC,
∵PN∥BC,PC∥NE,
∴四边形PCEN是平行四边形,
∴PN=EC,
∴PN
BM,
∴四边形BMNP是平行四边形.
 证明:过点N作NE⊥BC延长线于点E,
证明:过点N作NE⊥BC延长线于点E,∵∠AMN=90°,
∴∠AMB+∠EMN=90°,
∵∠BAM+∠BMA=90°,
∴∠BAM=∠NME,
在△ABM和△MEN中,
|
∴△ABM≌△MEN(AAS),
∴AB=ME=BC,
则BM=EC,
∵PN∥BC,PC∥NE,
∴四边形PCEN是平行四边形,
∴PN=EC,
∴PN
| ∥ |
. |
∴四边形BMNP是平行四边形.
看了 如图,在正方形ABCD中,点...的网友还看了以下:
D是线段AB的中点,C是线段AB的中垂线上一点,DE垂直AC于E,DF垂直BC于F.点C运动到什么 2020-04-27 …
关于点的对称问题已知点A关于点P(0,3)的对称点是B,B关于点Q(1,5/2)的对称点是C,点C 2020-05-02 …
超难的题目,我没有图.可不可以自己画图然后解出来?已知线段AB等于20cm,点C是AB的中点,点D 2020-05-13 …
如图,抛物线y=ax2+bx+c(a<0)与x轴相交于A、B两点,与y轴的正半轴相交于点C,对称轴 2020-05-15 …
过第四象限的直线与抛物线交于点A(0,3)和和点C,已知点C是抛物线的顶点,且抛物线的对称轴与Y粥 2020-05-16 …
AB是圆O的直径,BM垂直于AB于B点,点C是射线BM上异于端点的一动点,AC交圆O于D点,过D点 2020-05-16 …
AB是半圆O的直径,CO⊥AB交半圆O于点C,连结AC,⊙O’与OC,AB及半圆O相切于E,F,G 2020-06-06 …
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=1x(x<0)图象上一点,AO的延 2020-06-08 …
如图,已知一次函y=x-1的图象与x轴、y轴分别交于点A、B,点P是y轴上的任意一点,点C是一次函 2020-06-14 …
(2014•舟山)如图,在平面直角坐标系中,A是抛物线y=12x2上的一个动点,且点A在第一象限内 2020-06-14 …