早教吧作业答案频道 -->数学-->
设双曲线C的中心为点O,若有且只有一对相交于点O、所成的角为60°的直线A1B1和A2B2,使|A1B1|=|A2B2|,其中A1
题目详情
设双曲线C的中心为点O,若有且只有一对相交于点O、所成的角为60°的直线A1B1和A
B2,使|A1B1|=|A
B2|,其中A1、B1和A2、B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是___.
| 2 | |
| 2 | |
▼优质解答
答案和解析
不妨设双曲线的方程是
-
=1(a>0,b>0),
由|A1B1|=|A2B2|及双曲线的对称性知A1,A2,B1,B2关于x轴对称,如图,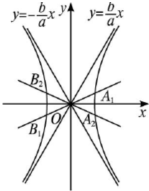
又∵满足条件的直线只有一对,
当直线与x轴夹角为30°时,双曲线的渐近线与x轴夹角大于30°,
双曲线与直线才能有交点A1,A2,B1,B2,
若双曲线的渐近线与x轴夹角等于30°,则无交点,
且不可能存在|A1B1|=|A2B2|,
当直线与x轴夹角为60°时,双曲线渐近线与x轴夹角小于60°,
双曲线与直线有一对交点A1,A2,B1,B2,
若双曲线的渐近线与x轴夹角等于60°,也满足题中有一对直线,
但是如果大于60°,则有两对直线.不符合题意,
∴tan30°<
≤tan60°,则
<
≤3,
∵b2=c2-a2,∴
<
≤3,
解得e∈(
,2].
故答案为(
,2].
| x2 |
| a2 |
| y2 |
| b2 |
由|A1B1|=|A2B2|及双曲线的对称性知A1,A2,B1,B2关于x轴对称,如图,

又∵满足条件的直线只有一对,
当直线与x轴夹角为30°时,双曲线的渐近线与x轴夹角大于30°,
双曲线与直线才能有交点A1,A2,B1,B2,
若双曲线的渐近线与x轴夹角等于30°,则无交点,
且不可能存在|A1B1|=|A2B2|,
当直线与x轴夹角为60°时,双曲线渐近线与x轴夹角小于60°,
双曲线与直线有一对交点A1,A2,B1,B2,
若双曲线的渐近线与x轴夹角等于60°,也满足题中有一对直线,
但是如果大于60°,则有两对直线.不符合题意,
∴tan30°<
| b |
| a |
| 1 |
| 3 |
| b2 |
| a2 |
∵b2=c2-a2,∴
| 1 |
| 3 |
| c2-a2 |
| a2 |
解得e∈(
2
| ||
| 3 |
故答案为(
2
| ||
| 3 |
看了 设双曲线C的中心为点O,若有...的网友还看了以下:
已知θ∈[0,π2],则直线y=xsinθ+1的倾斜角的取值范围是()A.[0,π2]B.[0,π 2020-04-11 …
若直线l经过第二、四象限,则直线l的倾斜角的范围()A.[0,π2)B.[0,π)C.[π2,π) 2020-04-11 …
直线xcosα-y+1=0的倾斜角的取值范围是()A.[0,π2]B.[0,π)C.[π4,3π4 2020-04-11 …
已知直线l仅经过第一、第三象限,则直线l的倾斜角的取值范围是()A.[0,π2)B.[π2,π)C 2020-04-11 …
1.已知a+b+c=0,a^2+b^2+c^=1,求:①ab+bc+ac的值②a^4+b^4+c^ 2020-07-09 …
若直线l经过第二、四象限,则直线l的倾斜角的范围()A.[0,π2)B.[0,π)C.[π2,π) 2020-07-18 …
一个数学问题whichsetsoforderedpairsrepresentfunctionsfr 2020-08-01 …
设A,B是非空集合,定义A*B={x|xAUB,且x不属于AnB}(1)已知A={x|0≤x≤2} 2020-08-01 …
如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=2 2020-08-01 …
若直线l经过第一二四象限,则直线l的倾斜角范围是A[0,pai/2]B[pai/2,pai]C(p 2020-08-03 …