早教吧作业答案频道 -->数学-->
如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直
题目详情
如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).
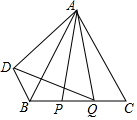
(1)当PQ=BD时,t=___s;
(2)求证:△ACP≌△ABQ;
(3)求证:△ADQ是等边三角形.

(1)当PQ=BD时,t=___s;
(2)求证:△ACP≌△ABQ;
(3)求证:△ADQ是等边三角形.
▼优质解答
答案和解析
(1) 由题意可知:BP=2t,BQ=2t
∴PQ=|2-4t|
∵点P关于直线AB的对称点为D,
∴BP=BD
∴当PQ=BD时,有:|2-4t|=2t,t=
或1;
即:当PQ=BD时,t=
或1,
故答案为:
或1.
(2)证明:∵△ABC是等边三角形,
∴AB=AC,∠ABQ=∠ACP=60°
在△ACP与△ABQ中,
,
∴△ACP≌△ABQ(SAS)
(3)证明:如图:
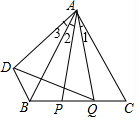
在△ABP与△ACQ中,
,
∴△ABP≌△ACQ(SAS)
又点P关于直线AB的对称点为D,
∴BD=BP,∠ABD=∠ABP
∴在△ABD与△ABP中,
,
∴△ABD≌△ABP(SAS)
∴△ACQ≌△ABD
∴∠1=∠3,AQ=AP=AD
∵∠1+∠BAQ=∠3+∠BAQ=60°
即:∠DAQ=60°.
∴△ADQ是等边三角形.
∴PQ=|2-4t|
∵点P关于直线AB的对称点为D,
∴BP=BD
∴当PQ=BD时,有:|2-4t|=2t,t=
| 1 |
| 3 |
即:当PQ=BD时,t=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
(2)证明:∵△ABC是等边三角形,
∴AB=AC,∠ABQ=∠ACP=60°
在△ACP与△ABQ中,
|
∴△ACP≌△ABQ(SAS)
(3)证明:如图:

在△ABP与△ACQ中,
|
∴△ABP≌△ACQ(SAS)
又点P关于直线AB的对称点为D,
∴BD=BP,∠ABD=∠ABP
∴在△ABD与△ABP中,
|
∴△ABD≌△ABP(SAS)
∴△ACQ≌△ABD
∴∠1=∠3,AQ=AP=AD
∵∠1+∠BAQ=∠3+∠BAQ=60°
即:∠DAQ=60°.
∴△ADQ是等边三角形.
看了 如图,△ABC是等边三角形,...的网友还看了以下:
已知Rt△ABC中,角B=90°,角A=60°,AB=2根号3cm,点O从C出发,沿CB以每秒1c 2020-05-13 …
将欲停分离器进油量保持不变,按停运分离器操作规程停运欲停分离器。 2020-05-31 …
随着时间的推移,地球上的板块运动会最终停止吗?地球构造发展成什么样子了之后,板块运动才会停止呢?板 2020-06-03 …
如图,小球从斜面上A处由静止滚下,经过B处,最终停在粗糙水平面上的C处.下列说法错误的是()A.小 2020-07-01 …
如图是2016年巴西里约热内卢第31届奥运会的会徽.在历史上曾经有三届奥运会因故停办,分别是191 2020-07-02 …
某质点做匀减速直线运动,依次经过A、B、C三点,最后停在D点.已知AB=6m,BC=4m,从A点运 2020-07-10 …
等腰△ABC的底长BC为32cm,腰长为20cm,一动点P在底边上从B向C以1cm/秒的速度移动, 2020-07-26 …
(2013•福州质检)如图,Rt△ABC中,∠C=90°,AC=BC=8,DE=2,线段DE在AC 2020-07-30 …
如图,矩形ABCD中,AB=12cm,BC=8cm,E为CD的中点.点P从A点出发,沿A-B-C的方 2020-11-01 …
以下关于热运动的说法正确的是()A.水流速度越大,水分子的热运动越剧烈B.水凝结成冰后,水分子的热运 2020-11-10 …