如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是AB上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是()A.1≤MI≤3B.32≤MI≤1C.12≤MI≤32D.3-1
如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是
上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
AB 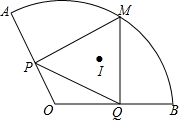
A. 1≤MI≤3
B.
≤MI≤13 2
C.
≤MI≤1 2 3 2
D.
-1≤MI≤13
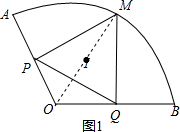 ①当点P,Q分别为OA,OB的中点时,MI有最大值,
①当点P,Q分别为OA,OB的中点时,MI有最大值,如图1,连接OM,PI,
∵∠AOB=120°,OP=OQ,
∴∠OPQ=∠OQP=30°,
∵MP⊥OA于P,MQ⊥OB于Q,
∴∠MPQ=∠MQP=60°,
∴△PQM是等边三角形,
∵I是△MPQ的内心,
∴OM过点I,
∴IM=OI=
| 1 |
| 2 |
②当P或Q与O重合时,IM有最小值,如图2,过作IE⊥PQ,IF⊥MQ,
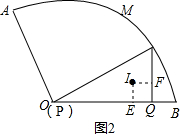
则四边形IEQF是正方形,
∵I是△MPQ的内心,
∴IF是内切圆的半径,∠IMQ=30°,
∴IF=
| 1 |
| 2 |
∵∠AOB=120°,MP⊥OA,
∴∠MPQ=30°,
∵PM=2,
∴PQ=
| 3 |
∴IF=
| ||
| 2 |
∴MI=
| 3 |
∴MI的长度的范围是:
| 3 |
故选D.
关于圆的一道题目(图很难画,P1是一块半径为1的半圆形纸板,在P1的坐下端剪去一个半径为1/2的半 2020-04-25 …
求方程(xy+y+sinx)dx+(x+cosy)dy=0的通解1,在半径为R的半球形立体的底面大 2020-05-17 …
在半径为1的半圆OAB上任取一点P,求点P到点A的距离大于1的概率. 2020-05-21 …
圆1的半径为2,p为圆外的一点,op长为3,那么以p为圆心,且与圆1相切的圆的半径为圆1的半径为2 2020-06-02 …
以O为圆心的两个同心圆的半径分别为11cm和9cm,若圆P与这两个圆都相切(1)问符合条件的圆P有 2020-07-08 …
(2014•槐荫区一模)如图,点P(m,n)为抛物线y=-12x2-x+1上的任意一点,以点P为圆 2020-07-26 …
对半导体言,其正确的说法是?(1)P型半导体中由于多数载流子为空穴,所以它带正电.(2)N型半导体 2020-07-29 …
已知一高斯光束在某点波面的半宽度为W及该处的曲率半径为R,证明该光束的腰部位于该波面左边的距离ζ= 2020-07-31 …
以O为圆心的两个同心圆的半径长分别是11cm和9cm,圆P与这两个圆相切(1)问符合条件的圆P有几 2020-08-01 …
如图所示,电阻R=1Ω、半径r1=0.2m的单匝圆形导线框P内有一个与P共面的圆形磁场区域Q,P、Q 2020-11-01 …