如图，某城市有一个五边形的地下污水管通道ABCDE，四边形BCDE是矩形，其中CD=8km，BC=3km；△ABE是以BE为底边的等腰三角形，AB=5km．现欲在BE的中间点P处建地下污水处理中心，为此要过点P建一

Question

如图，某城市有一个五边形的地下污水管通道ABCDE，四边形BCDE是矩形，其中CD=8km，BC=3km；△ABE是以BE为底边的等腰三角形，AB=5km．现欲在BE的中间点P处建地下污水处理中心，为此要过点P建一个“直线型”的地下水通道MN接通主管道，其中接口处M点在矩形BCDE的边BC或CD上．

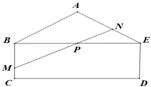
（1）若点M在边BC上，设∠BPM=θ，用θ表示BM和NE的长；
（2）点M设置在哪些地方，能使点M，N平分主通道ABCDE的周长？请说明理由．

Answer 1

（1）当点M在边BC上，设∠BPM=θ(0≤tanθ≤(3)/(4))，
在Rt△BPM中，BM=BP•tanθ=4tanθ．
在△PEN中，不妨设∠PEN=α，其中sinα=(3)/(5)，cosα=(4)/(5)，则(PE)/(sin(π-θ-α))=(NE)/(sinθ)，
即NE=(4sinθ)/(sin(θ+α))=(20sinθ)/(4sinθ+3cosθ)=(20tanθ)/(4tanθ+3)；

（2）当点M在边BC上，由BM+AB+AN=MC+CD+DE+EN，BM-NE=2；
即2tanθ-(10tanθ)/(4tanθ+3)=1；即8tan²θ-8tanθ-3=0，解得tanθ=(2±√(10))/(4)．
∵tanθ=(2-√(10))/(4)<0，tanθ=(2+√(10))/(4)>(3)/(4)与0≤tanθ≤(3)/(4)矛盾，点只能设在CD上．
当点M在边CD上，设CD中点为Q，由轴对称不妨设M在CQ上，此时点N在线段AE上；设∠MPQ=θ(0≤tanθ≤(4)/(3))，
在Rt△MPQ中，MQ=PQ•tanθ=3tanθ；
在△PAN中，不妨设∠PAE=β，其中sinβ=(4)/(5)，cosβ=(3)/(5)；
则(PA)/(sin(π-θ-β))=(AN)/(sinθ)，即AN=(3sinθ)/(sin(θ+β))=(15sinθ)/(3sinθ+4cosθ)=(15tanθ)/(3tanθ+4)；
由MC+CB+BA+AN=MQ+QD+DE+EN，得AN=MQ，即3tanθ=(15tanθ)/(3tanθ+4)；解得tanθ=0或tanθ=(1)/(3)；
故当CM=4，或者CM=4-3×(1)/(3)=3时，符合题意．
答：当点M位于CD中点Q处，或点M到点C的距离为3km时，才能使点M，N平分地下水总通道ABCDE的周长．