早教吧作业答案频道 -->数学-->
在△ABC中,∠ABC=90°,D为△ABC内一动点,BD=a,CD=b(其中a,b为常数,且a<b).将△CDB沿CB翻折,得到△CEB.连接AE.(1)请在图(1)中补全图形;(2)若∠ACB=α,AE⊥CE,则∠AEB=;(
题目详情
在△ABC中,∠ABC=90°,D为△ABC内一动点,BD=a,CD=b(其中a,b为常数,且a<b).将△CDB沿CB翻折,得到△CEB.连接AE.
(1)请在图(1)中补全图形;
(2)若∠ACB=α,AE⊥CE,则∠AEB=___;
(3)在(2)的条件下,用含a,b,α的式子表示AE的长.
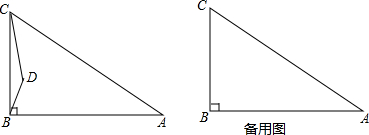
(1)请在图(1)中补全图形;
(2)若∠ACB=α,AE⊥CE,则∠AEB=___;
(3)在(2)的条件下,用含a,b,α的式子表示AE的长.

▼优质解答
答案和解析
(1)图象如图1所示,
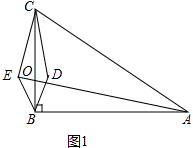
(2)结论:∠AEB=α.
理由:如图1中,设BC与AE交于点O,
∵AE⊥EC,
∴∠CEO=∠OBA,
∵∠EOC=∠BOA,
∴△EOC∽△OBA,
∴
=
,
∴
=
,∵∠EOB=∠COD,
∴△EOB∽△COA,
∴∠OEB=∠ACO=α.
故答案为α.
(3)如图2中,
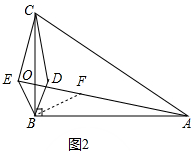
∵AE⊥CE
∴∠AEC=90°,
∵∠AEB=α,
∴∠BEC=90°+α,
过点B作BF⊥BE,交AE于点F,
则有∠FBE=90°.
即∠EBC+∠CBF=90°.
∵∠ABC=∠FBA+∠CBF=90°,
∴∠EBC=∠FBA.
∵∠BFA=∠AEB+∠EBF=90°+α.
∴∠BEC=∠BFA
∴△EBC∽△FBA.
∴
=
=
=tanα.
∵BD=a,CD=b,
∴BE=a,EC=b.
∴EF=
,AF=b•tanα.
∴AE=EF+AF=
+b•tanα.

(2)结论:∠AEB=α.
理由:如图1中,设BC与AE交于点O,
∵AE⊥EC,
∴∠CEO=∠OBA,
∵∠EOC=∠BOA,
∴△EOC∽△OBA,
∴
| EO |
| OB |
| CO |
| OA |
∴
| EO |
| OC |
| OB |
| OA |
∴△EOB∽△COA,
∴∠OEB=∠ACO=α.
故答案为α.
(3)如图2中,

∵AE⊥CE
∴∠AEC=90°,
∵∠AEB=α,
∴∠BEC=90°+α,
过点B作BF⊥BE,交AE于点F,
则有∠FBE=90°.
即∠EBC+∠CBF=90°.
∵∠ABC=∠FBA+∠CBF=90°,
∴∠EBC=∠FBA.
∵∠BFA=∠AEB+∠EBF=90°+α.
∴∠BEC=∠BFA
∴△EBC∽△FBA.
∴
| BA |
| BC |
| BF |
| BE |
| FA |
| EC |
∵BD=a,CD=b,
∴BE=a,EC=b.
∴EF=
| a |
| sinα |
∴AE=EF+AF=
| a |
| sinα |
看了 在△ABC中,∠ABC=90...的网友还看了以下:
卓越的人一大优点是:在不利与艰难的遭遇里百折不挠。这句名言告诉我们()A.挫折具有双重性B.挫折能 2020-04-07 …
人们之所以常说失败是成功之母、挫折孕育着成功,是因为[]A.不屈从于挫折的人会认真总结经验教训B. 2020-06-17 …
A,B,C三件衬衫的总价格为520元A、B、C三件衬衫的总价格为520元,若分别按9.5折、9折、 2020-06-22 …
有的人可以战胜挫折而功成名就,有的人却在挫折面前倒下了。这说明[]A.人们对待挫折的态度是不同的B 2020-07-01 …
下面加粗字的正确读音是1.曲折[]A.zh5B.zh62.倒影[]A.d3oB.d4o3.完好[]A 2020-10-31 …
下图漫画给我们的启示是()A.人生难免有挫折,挫折处处有B.每一个挫折对人都有双重影响C.人生的关键 2020-11-03 …
(2004•聊城模拟)某种T恤衫的进价为400元,出售时标价为600元,由于换季商店准备打折销售,但 2020-11-13 …
某商场店庆活动中,商家准备对某种进价为600元、标价为1200元的商品进行打折销售,但要保证利润率不 2020-11-13 …
2.“吃一堑,长一智。”这句话说明2.“吃一堑,长一智。”这句话说明A.挫折能够增长人的聪明才智B. 2020-12-19 …
挫折孕育着成功的含义是[]A.挫折能够增长人的聪明才智B.挫折可以激发进取精神C.挫折能增加人的胆量 2020-12-19 …