早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.(1)求∠ADB的度数;(2)判断△ABE的形状并加以证明;(3)连接DE,若DE⊥BD,DE=8,求AD的长.
题目详情
如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
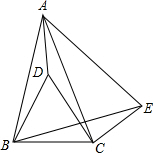
(1)求∠ADB的度数;
(2)判断△ABE的形状并加以证明;
(3)连接DE,若DE⊥BD,DE=8,求AD的长.

(1)求∠ADB的度数;
(2)判断△ABE的形状并加以证明;
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
▼优质解答
答案和解析
(1) ∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形,
∴DB=DC,∠BDC=∠DBC=∠DCB=60°,
在△ADB和△ADC中,
,
∴△ADB≌△ADC,
∴∠ADB=∠ADC,
∴∠ADB=
(360°-60°)=150°.
(2) 结论:△ABE是等边三角形.
理由:∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE,
在△ABD和△EBC中,
,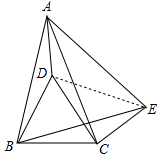
∴△ABD≌△EBC,
∴AB=BE,∵∠ABE=60°,
∴△ABE是等边三角形.
(3) 连接DE.
∵∠BCE=150°,∠DCB=60°,
∴∠DCE=90°,
∵∠EDB=90°,∠BDC=60°,
∴∠EDC=30°,
∴EC=
DE=4,
∵△ABD≌△EBC,
∴AD=EC=4.
∴△DBC是等边三角形,
∴DB=DC,∠BDC=∠DBC=∠DCB=60°,
在△ADB和△ADC中,
|
∴△ADB≌△ADC,
∴∠ADB=∠ADC,
∴∠ADB=
| 1 |
| 2 |
(2) 结论:△ABE是等边三角形.
理由:∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE,
在△ABD和△EBC中,
|

∴△ABD≌△EBC,
∴AB=BE,∵∠ABE=60°,
∴△ABE是等边三角形.
(3) 连接DE.
∵∠BCE=150°,∠DCB=60°,
∴∠DCE=90°,
∵∠EDB=90°,∠BDC=60°,
∴∠EDC=30°,
∴EC=
| 1 |
| 2 |
∵△ABD≌△EBC,
∴AD=EC=4.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
下面试题:11111111111对于化学反应A+B=C+D的下列说法中,正确的是()A.若A、B、 2020-04-27 …
在matlab中rank([A;B;C])=1是什么意思?已知向量A,B,C,若rank([A;B 2020-05-13 …
关于化学反应A+B=C+D,下列说法中正确的是A.若生成物C和D分别是盐和水,则反应物一定是酸和碱 2020-05-13 …
在反应A+B=C+D中,已知3克的A与5克的B恰好完全反应,生成2克的C,若生成D的质量为9克,则 2020-05-20 …
在△ABC和△AˊB′C′中,已知∠A=∠A′,AB=A′B′,在下面判断中错误的是()A.若添加 2020-05-23 …
关于化学反应A+B=C+D,下列说法中正确的是:A.若C是单质,D为化合物,则A和B中一定有一种是 2020-06-06 …
关于光现象,以下说法正确的是()A.你在岸边看到水中鱼的位置,其实就是鱼在水里的实际位置B.雨过天 2020-06-07 …
若三个非零且互不相等的实数a、b、c满足,则称a、b、c是调和的;若满a+c=2b足,则称a、b、 2020-06-10 …
设C点为后视点,D点为前视点,后视读数c=1.124m,前视读数d=1.428m,则().A.HC 2020-06-11 …