早教吧作业答案频道 -->数学-->
已知函数f（x）=ax+1，x≤0|lnx|，x>0当1<a<2时，关于x的方程f[f（x）]=a实数解的个数为（）A.2B.3C.4D.5
题目详情
已知函数f（x）=
当1<a<2时，关于x的方程f[f（x）]=a实数解的个数为（ ）ax+1，x≤0 |lnx|，x>0
A. 2
B. 3
C. 4
D. 5
▼优质解答
答案和解析
函数f（x）=
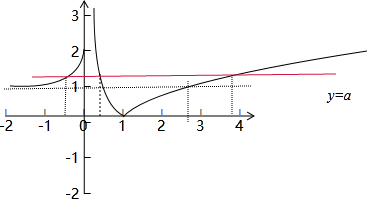
的图象如下，令f（t）=a，
∵1<a<2，如图所示得，方程f（t）=a有三个根：t1，t2，t3．
且t1<0，t2∈(e-2，e-1)，t3∈(e，e2)．
方程f（x）=t1无解，方程f（x）=t2有两个解，方程f（x）=t3无解．
故关于x的方程f[f（x）]=a实数解的个数为2，
故选：A．
函数f（x）=
|
∵1<a<2，如图所示得，方程f（t）=a有三个根：t1，t2，t3．
且t1<0，t2∈(e-2，e-1)，t3∈(e，e2)．
方程f（x）=t1无解，方程f（x）=t2有两个解，方程f（x）=t3无解．
故关于x的方程f[f（x）]=a实数解的个数为2，
故选：A．
看了 已知函数f（x）=ax+1，...的网友还看了以下：
初二的一道一元二次方程已知：关于x方程(m-1)x^2+mx+1=0……①,有两个相等的实数根求证 2020-04-27 …
求大虾们做两道数学题,一元二次方程那的.1、已知a ,b满足方程5a方+2007a+8=0 8b方 2020-05-16 …
已知关于x的一元二次方程【x的平方+(4m+1)x+2m-1=0】 （1）求证：不论m为任何实数, 2020-05-16 …
1.已知方程2x^2+mx-2m+1=0的两个实数根的平方和是7又四分之一.求m的值2.已知关于x 2020-05-16 …
方程kx平方减3x减1等0 有两个 不相等 的 实数根 则k的 取值范围是多少?关于 x的一元2次 2020-05-16 …
已知关于x的方程x方-2（k-3)x+k方-4k-1=0若这个方程有实数根,求k的取值范围若这个方 2020-05-16 …
一元二次方程题,杯具对于任意的非零实数m,关于x的方程x²-4x-m²=0的跟的情况是（从几个正负 2020-05-21 …
1,关于x的一元二次方程-x+(2k+1)x+2-k方=0有实数根,则K的取值范围?2,某种商品原 2020-06-02 …
设集合A=｛a|关于x的方程x方-2x+a=0有实数根,a属于R｝,B=｛a|关于x的方程ax方+ 2020-06-03 …
关于x的方程3x^2+4x-6/x+5=0有几个实数解,关于x的方程3x^2+4x-6/x+5=0 2020-06-27 …