早教吧作业答案频道 -->数学-->
如图,△ABC为等边三角形,点P是边AC的延长线上一点,连接BP,作∠BPQ等于60°,直线PQ与直线BC交于点N.(1)若点C平分AP时,求证:PB=PN;(2)若点C不平分时,求证:AP•PC=AB•CN;(3)
题目详情
如图,△ABC为等边三角形,点P是边AC的延长线上一点,连接BP,作∠BPQ等于60°,直线PQ与直线BC交于点N.
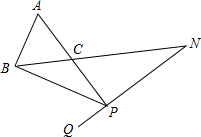
(1)若点C平分AP时,求证:PB=PN;
(2)若点C 不平分时,求证:AP•PC=AB•CN;
(3)若BC=2,CN=
,求∠N的正切值.

(1)若点C平分AP时,求证:PB=PN;
(2)若点C 不平分时,求证:AP•PC=AB•CN;
(3)若BC=2,CN=
| 3 |
| 2 |
▼优质解答
答案和解析
(1)证明:∵△ABC为等边三角形,
∴∠ACB=∠A=∠ABC=60°,BC=AC,
∴∠PCN=∠A=60°,
∵∠ACB=∠CBP+∠CPB=60°,∠BPQ=∠PBN+∠N=60°
∴∠CPB=∠N,
∵点C平分AP,
∴AC=PC,
∴BC=PC,
∴∠PBC=∠CPB,
∴∠PBC=∠N,
∴PB=PN;
(2)证明:由(1)得:∠PCN=∠A=60°,∠CPB=∠N,
∴△PAB∽△NCP,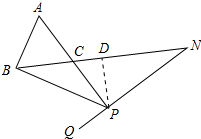
∴
=
,
∴AP•PC=AB•CN;
(3) 过点P作PD⊥CN于点D,如图所示:
∵△ABC为等边三角形,
∴AB=AC=BC=2,
由(1)知,AP•CP=AB•NC,
∴(PC+2)×PC=2×
,
整理得:PC2+2PC-3=0,
∴PC=1或PC=-3(舍去),
在Rt△PCD中,∠PDC=90°,∠PCD=60°
∴∠CPD=30°,
∴CD=
CP=
,
由勾股定理得:PD=
=
,
∴DN=CN-CD=
-
=1,
在Rt△NDP中,∠PDN=90°,tan∠N=
=
=
.
∴∠ACB=∠A=∠ABC=60°,BC=AC,
∴∠PCN=∠A=60°,
∵∠ACB=∠CBP+∠CPB=60°,∠BPQ=∠PBN+∠N=60°
∴∠CPB=∠N,
∵点C平分AP,
∴AC=PC,
∴BC=PC,
∴∠PBC=∠CPB,
∴∠PBC=∠N,
∴PB=PN;
(2)证明:由(1)得:∠PCN=∠A=60°,∠CPB=∠N,
∴△PAB∽△NCP,

∴
| AP |
| CN |
| AB |
| PC |
∴AP•PC=AB•CN;
(3) 过点P作PD⊥CN于点D,如图所示:
∵△ABC为等边三角形,
∴AB=AC=BC=2,
由(1)知,AP•CP=AB•NC,
∴(PC+2)×PC=2×
| 3 |
| 2 |
整理得:PC2+2PC-3=0,
∴PC=1或PC=-3(舍去),
在Rt△PCD中,∠PDC=90°,∠PCD=60°
∴∠CPD=30°,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得:PD=
| PC2-CD2 |
| ||
| 2 |
∴DN=CN-CD=
| 3 |
| 2 |
| 1 |
| 2 |
在Rt△NDP中,∠PDN=90°,tan∠N=
| PD |
| ND |
| ||||
| 1 |
| ||
| 2 |
看了 如图,△ABC为等边三角形,...的网友还看了以下:
1.已有定义inta[10],*p;则正确的赋值语句是().A.p=100;B.p=a[5];C.p 2020-03-31 …
如图,OB是圆A的直径,A为圆心,OB=20.DP与圆相切于点D,DP垂直于PB,垂足为P,PB与 2020-04-26 …
半径为5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC∶CA=4∶3,点P在弧AB上运动,过 2020-05-13 …
半径为5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC:CA=4:3,点P在弧AB上运动,过 2020-05-13 …
已知二次函数y=ax^2+bx+c的图像经过点A(3,0),B(2,-3),C(0,-3)1.求此 2020-05-15 …
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD平行BC, 2020-05-16 …
谁能告诉我爱情公式爱情={[(F+Ch+P)/2]+[3(C+I)]/10}/[(5-SI)2+2 2020-05-21 …
A、B、C是数轴上三点,分别表示a、b、c三数,已知(a+2)^+|b-4|=0,(c+1)/3- 2020-06-27 …
初三数学题过圆O外一点P作圆O的两条切线PA,PB,切点分别为A,B,联结AB,在AB,PB,PA上 2020-12-07 …
如图,已知点C在⊙O上,AC=12AB,动点P与点C位于直径AB的异侧,点P在半圆弧AB上运动(不与 2021-01-12 …