早教吧作业答案频道 -->数学-->
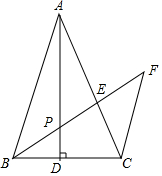
已知如图,在△ABC中,AB=AC,AD是垂线,P为AD上一点,过C做CF∥AB,延长BP交AC于E,交CF于F,求证:BP2=PE•PF.
题目详情
已知如图,在△ABC中,AB=AC,AD是垂线,P为AD上一点,过C做CF∥AB,延长BP交AC于E,交CF于F,求证:BP2=PE•PF.

▼优质解答
答案和解析
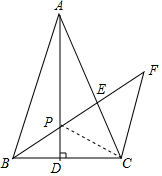 证明:连接PC,
证明:连接PC,
∵AB=AC,AD是中线,
∴AD是△ABC的对称轴.
∴PC=PB,∠PCE=∠ABP.
∵CF∥AB,
∴∠PFC=∠ABP(两直线平行,内错角相等),
∴∠PCE=∠PFC.
又∵∠CPE=∠EPC,
∴△EPC∽△CPF.
∴
=
(相似三角形的对应边成比例).
∴PC2=PE•PF.
∵PC=BP,
∴BP2=PE•PF.
 证明:连接PC,
证明:连接PC,∵AB=AC,AD是中线,
∴AD是△ABC的对称轴.
∴PC=PB,∠PCE=∠ABP.
∵CF∥AB,
∴∠PFC=∠ABP(两直线平行,内错角相等),
∴∠PCE=∠PFC.
又∵∠CPE=∠EPC,
∴△EPC∽△CPF.
∴
| PC |
| PE |
| PF |
| PC |
∴PC2=PE•PF.
∵PC=BP,
∴BP2=PE•PF.
看了 已知如图,在△ABC中,AB...的网友还看了以下:
1)已知平面内有4条直线a,b,c和d.直线a,b和c相交于一点.直线b,c和d也相交于一点,试确 2020-06-15 …
已知圆C经(x-1)2+(y-2)2=5经过椭圆E:x2a2+y2b2=1(a>b>0)的右焦点F 2020-06-21 …
如图,已知点B的坐标为(6,9),点A的坐标为(6,6),点P为⊙A上一动点,PB的延长线交⊙A于 2020-06-23 …
9.已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.若∠ 2020-07-14 …
已知抛物线y=ax+bx+3与x轴交点于A(1,0)B(-3,0)于y轴交点为C,若点E为第二象限 2020-07-20 …
如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线经过A 2020-07-22 …
如图已知ad是三角形ABC的中线,b,e交A,C于点e,交AD于点f且Ae东宇f一求AC等于BF 2020-07-22 …
已知点A(0,2),抛物线C:y2=2px(p>0)的焦点为F,射线FA与抛物线C相交于点M,与其 2020-07-29 …
如图,已知圆O1与圆O2相交于A,B两点,直线O1A交圆O1于C,交圆O2于D,连接CB并延长交圆O 2020-12-01 …
已知:如图,在锐角∠MAN的边AN上取一点B,以AB为直径的半圆O交AM于C,交∠MAN的角平分线于 2020-12-07 …