早教吧作业答案频道 -->数学-->
如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为()A.4B.3+2C.7+1D.23
题目详情
如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )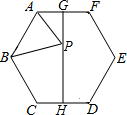
A. 4
B.
+23
C.
+17
D. 23
▼优质解答
答案和解析
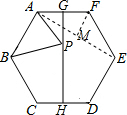 利用正多边形的性质可得点B关于GH的对称点为点E,连接AE交GH于点P,那么有PB=PE,AP+BP=AE最小.
利用正多边形的性质可得点B关于GH的对称点为点E,连接AE交GH于点P,那么有PB=PE,AP+BP=AE最小.
又易知△AEF为等腰三角形,∠AFE=120°,
则作FM⊥AE于点M,
∵∠AFE=120°,AF=EF,
∴∠FAE=∠FEA=30°,AM=EM,
在RT△AFM中,AF=2,
∴AM=
AF=
,
∴AM=EM=
,从而AE=2
,
故AP+BP的最小值为2
.
故选D.
 利用正多边形的性质可得点B关于GH的对称点为点E,连接AE交GH于点P,那么有PB=PE,AP+BP=AE最小.
利用正多边形的性质可得点B关于GH的对称点为点E,连接AE交GH于点P,那么有PB=PE,AP+BP=AE最小.又易知△AEF为等腰三角形,∠AFE=120°,
则作FM⊥AE于点M,
∵∠AFE=120°,AF=EF,
∴∠FAE=∠FEA=30°,AM=EM,
在RT△AFM中,AF=2,
∴AM=
| ||
| 2 |
| 3 |
∴AM=EM=
| 3 |
| 3 |
故AP+BP的最小值为2
| 3 |
故选D.
看了 如图,已知正六边形ABCDE...的网友还看了以下:
两个点电荷,电量分别是q1=4x10^-9c、q2=9x10-9c,两者固定于相距20cm的a、b 2020-05-21 …
固定的A和B两个点电荷都带正电,相距8cm,今将第三个点电荷C放在A与B连线上A的内侧A电荷2cm 2020-06-16 …
两个等量的异种电荷A和B连线上的电场强度大小是如何变化的?为什么? 2020-07-20 …
如图所示,电荷量均为+Q的点电荷A、B连线上有a、c两点,在连线的中垂线上有b、d两点,a、b、c 2020-07-21 …
如图,A、B为两等量异号点电荷,A带正电,B带负电,在A、B连线上有a、b、c三点,其中b为连线的 2020-07-30 …
如图所示是单色光双缝干涉实验某一时刻的波形图,实线表示波峰,虚线表示波谷.在此时刻,介质中A点为波 2020-08-01 …
读“上海市及上海港位置示意图”,回答下列问题。(7分)(1)图中字母代表的地理事物名称:铁路线A卫星 2020-11-04 …
如图所示,在“用描迹法画出电场中平面上的等势线”的实验中:(1)在平板上应先先铺上白纸,再铺上,最后 2020-11-10 …
在光滑的绝缘水平面上,相隔2L的A、B两点固定有两个电量均为Q的正点电荷,a、O、b是A、B连线上的 2020-11-25 …
两个函数差的连续区间怎么求出来的?设函数f(x)在[a,b]上连续,F(x)=f(x)-f(x+(b 2020-11-28 …