早教吧作业答案频道 -->数学-->
如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.(1)求证:∠BAC=90°;(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,请求出BP的长.
题目详情
如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.
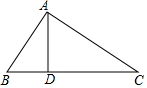
(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,请求出BP的长.

(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,请求出BP的长.
▼优质解答
答案和解析
(11)证明:△ABC是直角三角形,理由如下:
∵AD⊥BC,AD=4,BD=2,
∴AB2=AD2+BD2=20,
又∵AD⊥BC,CD=8,AD=4,
∴AC2=CD2+AD2=80,
∵BC=CD+BD=10,
∴BC2=100,
∴AC2+AB2=100=BC2,
∴∠BAC=90°,△ABC是直角三角形.
(2) 分三种情况:
①当BP=AB时,
∵AD⊥BC,
∴AB=
=2
,
∴BP=AB=2
;
②当BP=AP时,P我BC的中点,
∴BP=
AB=5;
③当AP=AB是,BP=2BD=4;
综上所述:BP的长为2
或5或4.
∵AD⊥BC,AD=4,BD=2,
∴AB2=AD2+BD2=20,
又∵AD⊥BC,CD=8,AD=4,
∴AC2=CD2+AD2=80,
∵BC=CD+BD=10,
∴BC2=100,
∴AC2+AB2=100=BC2,
∴∠BAC=90°,△ABC是直角三角形.
(2) 分三种情况:
①当BP=AB时,
∵AD⊥BC,
∴AB=
| BD2+AD2 |
| 5 |
∴BP=AB=2
| 5 |
②当BP=AP时,P我BC的中点,
∴BP=
| 1 |
| 2 |
③当AP=AB是,BP=2BD=4;
综上所述:BP的长为2
| 5 |
看了 如图,在△ABC中,AD⊥B...的网友还看了以下:
向量数量积运算律的推理1、对于向量a、b、c,有①a·b=b·c不能推出a=c;②(a·b)≠a( 2020-05-16 …
J表示初中化学常见物质,A用于改良酸性土壤,G是红棕色粉末,E,K,J为无色气体RT,求推出 A, 2020-05-16 …
由a=b一定可以得出的等式是()A.a÷c=b÷c由a=b一定可以得出的等式是()A.a÷c=b÷ 2020-06-06 …
读我国“我国锋面雨带图”回答35~36题.影响我国长江流域出现空梅的原因是()A.D提前出现,A滞 2020-06-26 …
ABCD4个元素,以各种顺序进栈出栈.请问一共会有多少种情况.例如A进A出,B进B出,C进C出,D 2020-06-28 …
对于三个均不为0的数a,b,c,若ab=ac,则b=c.对于向量a,b,c,由a×b=a×c,能得 2020-07-20 …
已知a、b、c两两不等,且满足a^2+b^2+mab=b^2+c^2+mbc=c^2+a^2+mc 2020-07-20 …
(1)a>b>0,0>c>d推出a/c>b/d(2)a>b>0推出1/a>1/b(3)a>b>0推 2020-07-30 …
下面使用类比推理正确的是()A.直线a,b,c,若a∥b,b∥c,则a∥c.类推出:向量a,b,c, 2020-11-02 …
铝是常见的轻金属,它能发生下列变化:试回答:(1)上述变化中,具有两性的化合物是(填化学式)(2)上 2020-11-02 …