早教吧作业答案频道 -->数学-->
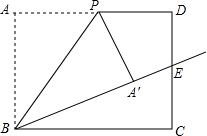
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为.
题目详情
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为___.

▼优质解答
答案和解析
∵四边形ABCD是矩形,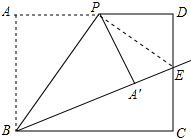
∴AD=BC=12,CD=AB=10,∠A=∠D=∠C=90°,
∵E是CD的中点,
∴DE=CE=5,
∴BE=
=
=13,
由折叠的性质得:∠BAP′=∠A=90°,BA′=BA=10,PA′=PA,
∴∠PA′E=90°,A′E=13-10=3,
连接PE,如图所示:
设PA′=PA=x,则PD=12-x,
由勾股定理得:PE2=PA′2+A′E2=PD2+DE2,
即x2+32=(12-x)2+52,
解得:x=
,
∴PA′=
,PD=12-
=
,
∴四边形DPA′E的面积=
×3×
+
×5×
=
;
故答案为:
.

∴AD=BC=12,CD=AB=10,∠A=∠D=∠C=90°,
∵E是CD的中点,
∴DE=CE=5,
∴BE=
| BC2+CE2 |
| 122+52 |
由折叠的性质得:∠BAP′=∠A=90°,BA′=BA=10,PA′=PA,
∴∠PA′E=90°,A′E=13-10=3,
连接PE,如图所示:
设PA′=PA=x,则PD=12-x,
由勾股定理得:PE2=PA′2+A′E2=PD2+DE2,
即x2+32=(12-x)2+52,
解得:x=
| 20 |
| 3 |
∴PA′=
| 20 |
| 3 |
| 20 |
| 3 |
| 16 |
| 3 |
∴四边形DPA′E的面积=
| 1 |
| 2 |
| 20 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
| 70 |
| 3 |
故答案为:
| 70 |
| 3 |
看了 如图,在矩形ABCD中,AB...的网友还看了以下:
在矩形ABCD中,AD//BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E F, 2020-05-16 …
滑动变阻器的连接?滑片P往左(A,B和C,D和A,C和A,D和B,C和B,D)请一一告诉我他们哪些 2020-05-20 …
钻杆柱的重要作用是传递(),输送工作液,完成修井工艺要求。A.扭矩B.动力C.速度D.路程 2020-05-31 …
气动浮球式液位变送器是一种( )平衡式仪表。A.力矩B.能量C.压力D.浮力 2020-06-07 …
全浮式支承的半轴多为整体式,半轴与桥壳没有直接联系,半轴承受( )A.弯矩B.转矩C.弯矩和其他的力 2020-06-07 …
如图,矩形ABCD的周长为8,设AB=x(1≤x≤3),线段MN的两端点在矩形的边上滑动,且MN= 2020-06-22 …
公式难题,abcdefgn分别为不等的数值.a+b+n=?a+c+n=?a+d+n=?……………… 2020-08-04 …
已知a、b的阳离子和c、d的阴离子电子层结构相同,且原子半径a>b,阴离子所带电荷数c>d,则它们的 2020-11-26 …
一、能证明的证明,不能的举反例哦!1、如果a>b,判断a-c与b-c的大小2、如果a>b,cb,c> 2020-11-27 …
公式难题...abcdefgn分别为不等的数值.a+b+n=?a+c+n=?a+d+n=?…………… 2020-11-28 …