早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.(1)求证:AC是O的切线;(2)若OB=10,CD=8,求CE的长.
题目详情
如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
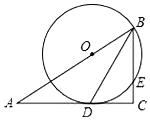
(1)求证:AC是 O的切线;
(2)若OB=10,CD=8,求CE的长.

(1)求证:AC是 O的切线;
(2)若OB=10,CD=8,求CE的长.
▼优质解答
答案和解析
(1)证明:连接OD,如图,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
∴AC是 O的切线;
(2) 过O作OG⊥BC,连接OE,
则四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
解得:BE=12,
∵AC是 O的切线,
∴CD2=CE•CB,
即82=CE(CE+12),
解得:CE=4或CE=-16(舍去),
即CE的长为4.
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,

∴∠ODA=90°,
∴AC是 O的切线;
(2) 过O作OG⊥BC,连接OE,
则四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
解得:BE=12,
∵AC是 O的切线,
∴CD2=CE•CB,
即82=CE(CE+12),
解得:CE=4或CE=-16(舍去),
即CE的长为4.
看了 如图,在Rt△ABC中,∠C...的网友还看了以下:
以下能正确表示芽接步骤顺序的是①在砧木树皮上切“T”形切口②接穗切成盾形芽片③将芽片插入“T”形切 2020-05-17 …
过双曲线x2a2−y2b2=1(a>0,b>0)的左焦点F1作圆x2+y2=a2的切线交双曲线右支 2020-07-14 …
据图所示,有关工具酶功能的叙述错误的是[]A.限制性核酸内切酶可以切断a处B.DNA聚合酶可以连接 2020-07-15 …
P为双曲线-=1上的一点,F为一个焦点,以PF为直径的圆与圆x2+y2=a2的位置关系是()A.内 2020-07-26 …
以双曲线的一条焦半径为直径的圆与以实轴为直径的圆的位置关系为()A.相交B.内切C.外切D.内切或 2020-07-26 …
数学圆的切线1.如图,在三角形ABC中,角BCA=90度,角A=30度,以AB为直径画圆O,延长A 2020-07-31 …
①能以小善中人之意②前后左右者日益亲③小信固人之心④图左右之亲近⑤急之则挟人主以为质⑥则惧祸之心日益 2020-11-28 …
为了落实“科教兴国”战略,青少年应该从自身做起,努力培养创新精神,要做到[]①勤于观察②善于思考③培 2020-11-29 …
古希腊神话中的大地女神该亚的故事,反映了人类社会早期[]①女人的权力位于男人之上②男人的权力开始超越 2020-12-25 …
据图所示,有关工具酶功能的叙述不正确的是()A.限制性内切酶可以切断a处B.DNA聚合酶可以连接a处 2021-01-13 …