早教吧作业答案频道 -->数学-->
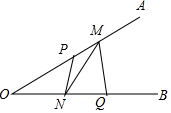
已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是.
题目详情
已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P-N-M-Q长度的最小值是___.

▼优质解答
答案和解析
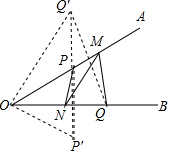 作P关于OB的对称点P′,作Q关于OA的对称点Q′,
作P关于OB的对称点P′,作Q关于OA的对称点Q′,
连接P′Q′,即为折线P-N-M-Q长度的最小值.
根据轴对称的定义可知:∠NOP′=∠AOB=30°,∠OPP′=60°,
∴△OPP′为等边三角形,△OQQ′为等边三角形,
∴∠P′OQ′=90°,
∴在Rt△P′OQ′中,
P′Q′=
=5.
故答案为5.
 作P关于OB的对称点P′,作Q关于OA的对称点Q′,
作P关于OB的对称点P′,作Q关于OA的对称点Q′,连接P′Q′,即为折线P-N-M-Q长度的最小值.
根据轴对称的定义可知:∠NOP′=∠AOB=30°,∠OPP′=60°,
∴△OPP′为等边三角形,△OQQ′为等边三角形,
∴∠P′OQ′=90°,
∴在Rt△P′OQ′中,
P′Q′=
| 32+42 |
故答案为5.
看了 已知∠AOB=30°,点P、...的网友还看了以下:
如图所示是固定在水平桌面上的粗糙圆弧轨道,将一小球由轨道的P点自由释放,小球滚动到Q点,然后又继续 2020-05-02 …
在直角梯形ABCD中,角B=90°,AD‖BC,且AD=4cm,AB=6cm,DC=10cm,若动 2020-05-16 …
如图所示,物体的质量为2kg,沿水平面向右运动,它与水平面的动摩擦因素为0.5,当物体运动到P点时 2020-05-17 …
如图所示,弹簧一端固定在竖直墙壁上,另一端连着物块,L0为弹簧原长(图中O点位置).开始时用外力把 2020-06-14 …
(2014•南京三模)如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,初始时刻小球静止于P点 2020-07-07 …
C1,C2是以原点为圆心的两个同心圆,C1的半径r1=2,C2的半径r2=6,C1上有一点P,C2 2020-08-01 …
如图所示,甲带电体固定在绝缘水平面上的O点.另一个电荷量为+q、质量为m的带电体乙,从P点由静止释放 2020-11-02 …
如图所示,一物块从一光滑且足够长的固定斜面顶端O点无初速释放后,先后通过P、Q、N三点,已知物块从P 2020-12-09 …
如图所示,x轴与水平传送带重合,坐标原点O在传送带的左端,传送带长L=8m,匀速运动的速度v0=5m 2020-12-12 …
1.一个质量为m的小球用长为L的细线悬挂于O点.小球在水平力F的作用下,从平衡位置P缓慢地移动到Q点 2021-01-02 …