早教吧作业答案频道 -->数学-->
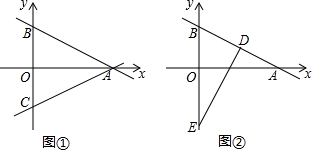
如图①,直线y=-12x+1分别与坐标轴交于A,B两点,在y轴的负半轴上截取OC=OB(1)求直线AC的解析式;(2)如图②,在x轴上取一点D(1,0),过D作DE⊥AB交y轴于E,求E点坐标.
题目详情
如图①,直线y=-
x+1分别与坐标轴交于A,B两点,在y轴的负半轴上截取OC=OB
(1)求直线AC的解析式;
(2)如图②,在x轴上取一点D(1,0),过D作DE⊥AB交y轴于E,求E点坐标.
| 1 |
| 2 |
(1)求直线AC的解析式;
(2)如图②,在x轴上取一点D(1,0),过D作DE⊥AB交y轴于E,求E点坐标.

▼优质解答
答案和解析
(1)y=-
x+1,
当x=0时,y=1,
当y=0时,x=2,
则点A的坐标为(2,0),点B的坐标为(0,1),
∵在y轴的负半轴上截取OC=OB,
∴点C的坐标为(0,-1),
设直线AC的解析式为y=kx+b,
把点A(2,0),C(0,-1)代入得:
解得:
∴y=
x-1.
(2)由直线AB的解析式为y=-
x+1,DE⊥AB,
设直线DE的解析式为y=
x+b,
把D(1,0)代入得:
+b=0,
解得:b=-
,
∴直线DE的解析式为y=
x-
,
当x=0时,y=-
,
∴点E的坐标为(0,-
).
| 1 |
| 2 |
当x=0时,y=1,
当y=0时,x=2,
则点A的坐标为(2,0),点B的坐标为(0,1),
∵在y轴的负半轴上截取OC=OB,
∴点C的坐标为(0,-1),
设直线AC的解析式为y=kx+b,
把点A(2,0),C(0,-1)代入得:
|
解得:
|
∴y=
| 1 |
| 2 |
(2)由直线AB的解析式为y=-
| 1 |
| 2 |
设直线DE的解析式为y=
| 1 |
| 2 |
把D(1,0)代入得:
| 1 |
| 2 |
解得:b=-
| 1 |
| 2 |
∴直线DE的解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
当x=0时,y=-
| 1 |
| 2 |
∴点E的坐标为(0,-
| 1 |
| 2 |
看了 如图①,直线y=-12x+1...的网友还看了以下:
在平面坐标系中 抛物线的解析式是y=1/4xx+1,点c的坐标为(-4.0),平行四边形oabc的 2020-05-16 …
已知两空间直角坐标系α,β,在α坐标系中有三点A(x1,y1,z1),B(x2,y2,z2),C( 2020-05-16 …
计算机硬件设备都要连接到()上.A鼠标B键盘C显示器D主板下列不属于计算机硬件的是A主板B主机箱C 2020-05-20 …
集合——thank已知集合A=(-2,0,1.,3),在平面直角坐标系中,点M的坐标(x,y)满足 2020-06-07 …
已知圆心坐标(a,b)和半径r,圆心角为C,求对应的圆上的坐标.求哪位达人给个公式,我忘完了,汗死 2020-06-12 …
如图直线y=2x+6分别与x轴、y轴相交于A、C两点(求出后A坐标为(-3,0)C坐标为(0,6) 2020-06-13 …
岛上A、B两块巨石的坐标分别是A(2,1)B(8,2),藏宝地坐标是(6,6),在上面的地图中画出 2020-06-14 …
一架匀速飞行的战斗机,为能击中地面上的目标,则投弹的位置是()A.在目标的正上方B.在飞抵目标之前 2020-06-16 …
关于向量标架的一道问题已知向量a,b,c的坐标如下:1、在标架{O;e1,e2}下,a={0,1} 2020-06-18 …
求自然数m,使得a(m-1),(am)2,a(m+1)+3依次成等差数列这里的上标下标显示不出来第 2020-07-23 …