早教吧作业答案频道 -->数学-->
如图，在四棱锥P-ABCD中，四边形ABCD为平行四边形，AC，BD相交于点O，点E为PC的中点，OP=OC，PA⊥PD．求证：（1）直线PA∥平面BDE；（2）平面BDE⊥平面PCD．
题目详情
如图，在四棱锥P-ABCD中，四边形ABCD为平行四边形，AC，BD相交于点O，点E为PC的中点，OP=OC，PA⊥PD．求证：
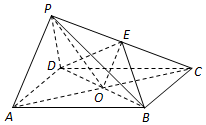
（1）直线PA∥平面BDE；
（2）平面BDE⊥平面PCD．
（1）直线PA∥平面BDE；
（2）平面BDE⊥平面PCD．
▼优质解答
答案和解析
证明：（1）连结OE，因为O为平行四边形ABCD对角线的交点，所以O为AC中点．
又因为E为PC的中点，
所以OE∥PA． …4分
又因为OE⊂平面BDE，PA⊄平面BDE，
所以直线PA∥平面BDE． …6分
（2）因为OE∥PA，PA⊥PD，所以OE⊥PD． …8分
因为OP=OC，E为PC的中点，所以OE⊥PC． …10分
又因为PD⊂平面PCD，PC⊂平面PCD，PC∩PD=P，
所以OE⊥平面PCD． …12分
又因为OE⊂平面BDE，所以平面BDE⊥平面PCD． …14分．
又因为E为PC的中点，
所以OE∥PA． …4分
又因为OE⊂平面BDE，PA⊄平面BDE，
所以直线PA∥平面BDE． …6分
（2）因为OE∥PA，PA⊥PD，所以OE⊥PD． …8分
因为OP=OC，E为PC的中点，所以OE⊥PC． …10分
又因为PD⊂平面PCD，PC⊂平面PCD，PC∩PD=P，
所以OE⊥平面PCD． …12分
又因为OE⊂平面BDE，所以平面BDE⊥平面PCD． …14分．
看了 如图，在四棱锥P-ABCD中...的网友还看了以下：
已知a/b=c/d.求证:a+c/b+d=a-c/b-d 2020-04-05 …
证明四点共圆.如图:证明C,B,D,E,四点共圆.标准答案的第一步：连接BE ,则AD×AB=AE 2020-05-13 …
是关于相似图形的性质的题!（1）已知a/b=c/d,求证a+c/b+a=a/b（2）已知a/b=c 2020-05-16 …
高一不等式已知a>b,c>d,求证a+c>b+d详细过程.谢谢 2020-06-10 …
已知a、b、c都是实数,且（a²+b²）x²-2b(a+c)x+b²+c=0,试证明c/b=b/a 2020-06-27 …
已知1/a,1/b,1/c,成等差数列,求证,(a+c)/b是(b+c)/a与(a+b)/c的等差 2020-08-02 …
证明反比性质和更比性质1.如果a/b=c/d,求证b/a=d/c.2.如果a/b=c/d,求证a/c 2020-10-30 …
已知a大于0,b大于0,c大于0,d大于0,且a\b大于c\d,求证a+c\b+d大于c\d 2020-11-01 …
阅读课本材料，解答后面的问题．折纸与证明折纸，常常能为证明一个命题提供思路和方法．例如，在△ABC中 2020-11-28 …
已知a>b,c>b,求证a+c>b+d还有二分之五-x>三分之一,则x 2020-12-17 …