早教吧作业答案频道 -->数学-->
如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC(1)求抛物线的解析式;(2)将直线CD绕点C逆时针方向旋转45°,所得直线与抛物线线相交
题目详情
如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC
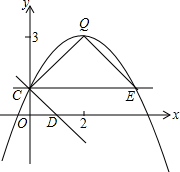
(1)求抛物线的解析式;
(2)将直线CD绕点C逆时针方向旋转45°,所得直线与抛物线线相交于另一点E,求证:△CEQ∽△CDO;
(3)①在(2)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②直线写出将该抛物线沿QC方向平移
个单位后的抛物线的解析式.

(1)求抛物线的解析式;
(2)将直线CD绕点C逆时针方向旋转45°,所得直线与抛物线线相交于另一点E,求证:△CEQ∽△CDO;
(3)①在(2)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②直线写出将该抛物线沿QC方向平移
| 2 |
▼优质解答
答案和解析
(1)设抛物线的解析式为y=a(x-2)2+3,
将C(0,1)代入得:1=a×(-2)2+3,
解得a=-
.
∴y=-
(x-2)2+3=-
x2+2x+1.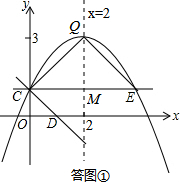
(2)证明:由题意可知,∠ECD=45°,
∵OC=OD,且OC⊥OD,
∴△OCD为等腰直角三角形,∠ODC=45°,
∴∠ECD=∠ODC,
∴CE∥x轴,则点C、E关于对称轴(直线x=2)对称,
∴点E的坐标为(4,1).
如答图①所示,设对称轴(直线x=2)与CE交于点M,则M(2,1),
∴ME=CM=QM=2,
∴△QME与△QMC均为等腰直角三角形,
∴∠QEC=∠QCE=45°.
又∵△OCD为等腰直角三角形,
∴∠ODC=∠OCD=45°,
∴∠QEC=∠QCE=∠ODC=∠OCD=45°,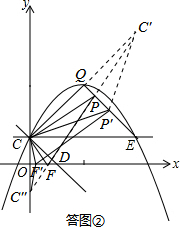
∴△CEQ∽△CDO.
(3)①存在.
如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.
(证明如下:不妨在线段OD上取异于点F的任一点F′,在线段QE上取异于点P的任一点P′,连接F′C″,F′P′,P′C′.
由轴对称的性质可知,△P′CF′的周长=F′C″+F′P′+P′C′;
而F′C″+F′P′+P′C′是点C′,C″之间的折线段,
由两点之间线段最短可知:F′C″+F′P′+P′C′>C′C″,
即△P′CF′的周长大于△PCE的周长.)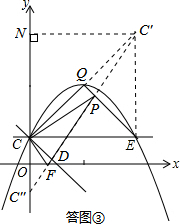
如答图③所示,连接C′E,
∵C,C′关于直线QE对称,△QCE为等腰直角三角形,
∴△QC′E为等腰直角三角形,
∴△CEC′为等腰直角三角形,
∴点C′的坐标为(4,5);
∵C,C″关于x轴对称,∴点C″的坐标为(0,-1).
过点C′作C′N⊥y轴于点N,则NC′=4,NC″=4+1+1=6,
在Rt△C′NC″中,由勾股定理得:C′C″=
=
=2
.
综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为2
.
②∵C(0,1),Q(2,3),
∴可得∠QCE=45°,则将该抛物线沿QC方向平移
个单位后的抛物线的解析式相当于向下平移-1个单位,
再向左平移1个单位得到的函数解析式,故平移后解析式为:y=-
(x-1)2+2.
将C(0,1)代入得:1=a×(-2)2+3,
解得a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
| 1 |
| 2 |

(2)证明:由题意可知,∠ECD=45°,
∵OC=OD,且OC⊥OD,
∴△OCD为等腰直角三角形,∠ODC=45°,
∴∠ECD=∠ODC,
∴CE∥x轴,则点C、E关于对称轴(直线x=2)对称,
∴点E的坐标为(4,1).
如答图①所示,设对称轴(直线x=2)与CE交于点M,则M(2,1),
∴ME=CM=QM=2,
∴△QME与△QMC均为等腰直角三角形,
∴∠QEC=∠QCE=45°.
又∵△OCD为等腰直角三角形,
∴∠ODC=∠OCD=45°,
∴∠QEC=∠QCE=∠ODC=∠OCD=45°,

∴△CEQ∽△CDO.
(3)①存在.
如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.
(证明如下:不妨在线段OD上取异于点F的任一点F′,在线段QE上取异于点P的任一点P′,连接F′C″,F′P′,P′C′.
由轴对称的性质可知,△P′CF′的周长=F′C″+F′P′+P′C′;
而F′C″+F′P′+P′C′是点C′,C″之间的折线段,
由两点之间线段最短可知:F′C″+F′P′+P′C′>C′C″,
即△P′CF′的周长大于△PCE的周长.)

如答图③所示,连接C′E,
∵C,C′关于直线QE对称,△QCE为等腰直角三角形,
∴△QC′E为等腰直角三角形,
∴△CEC′为等腰直角三角形,
∴点C′的坐标为(4,5);
∵C,C″关于x轴对称,∴点C″的坐标为(0,-1).
过点C′作C′N⊥y轴于点N,则NC′=4,NC″=4+1+1=6,
在Rt△C′NC″中,由勾股定理得:C′C″=
| C′N2+C″N2 |
| 42+62 |
| 13 |
综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为2
| 13 |
②∵C(0,1),Q(2,3),
∴可得∠QCE=45°,则将该抛物线沿QC方向平移
| 2 |
再向左平移1个单位得到的函数解析式,故平移后解析式为:y=-
| 1 |
| 2 |
看了 如图,抛物线y=ax2+bx...的网友还看了以下:
(2012•资阳)根据图中小磁针静止时的指向,用笔划线代替导线将如图所示的实物连线图补充完整(要求 2020-05-13 …
图①,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM、CN 2020-06-12 …
以直线MN为对称轴,作图A的轴对称图形,得到图形B.将图形B绕点O顺时针旋转90°,得到图形C.将 2020-08-01 …
在下列方格中画一画.①将图形A绕点O顺时针旋转90°,得到图形B.②将图形B向右平移5个方格得到图 2020-08-03 …
(1)将上面的图形A向右平移10格,得到图形B.(2)以直线L为对称轴,作图形A的轴对称图形.得到 2020-08-03 …
AB是一段火车先行驶的路线图,A,C,D,B表示4个火车站在这段路线上往返行车,需印制几种车票?有 2020-08-04 …
如图所示是通电螺线管周围四个小磁针(图中涂黑的一端是N极)静止时指向,其中正确的是()A.a磁针B. 2020-11-01 …
洛川会议通过了《抗日救国十大纲领》,主要内容是:……(2)实施全国军事的总动员;(3)实施全国人民的 2020-11-30 …
如图所示有一闭合导线环,磁场方向垂直环面向里,当磁感应强度随时间一直均匀增大时,顺着磁场方向看导线环 2020-12-05 …
下列与抗日民族统一战线初步建成相关的事件中,起决定作用的是[]A.中共发表八一宣言,号召停止内战,一 2020-12-28 …