早教吧作业答案频道 -->数学-->
如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.(1)在图1中,∠AOC=,∠BOC=.(2)将
题目详情
如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
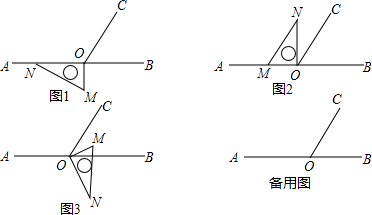
(1)在图1中,∠AOC=___,∠BOC=___.
(2)将图1中的三角板按图2的位置放置,使得OM在射线OA上,则∠CON=___;
(3)将上述直角三角板按图3的位置放置,使得OM在∠BOC的内部,求∠BON-∠COM的度数.

(1)在图1中,∠AOC=___,∠BOC=___.
(2)将图1中的三角板按图2的位置放置,使得OM在射线OA上,则∠CON=___;
(3)将上述直角三角板按图3的位置放置,使得OM在∠BOC的内部,求∠BON-∠COM的度数.
▼优质解答
答案和解析
(1)∵点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,
∴∠AOC=120°,∠BOC=60°
故答案为:120°,60°;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC-∠MON=120°-90°=30°,
故答案为:30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,
则,∠BON-∠COM=90°-∠BOM-(60°-∠BOM)=30°,
即∠BON-∠COM的度数是30°.
∴∠AOC=120°,∠BOC=60°
故答案为:120°,60°;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC-∠MON=120°-90°=30°,
故答案为:30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,
则,∠BON-∠COM=90°-∠BOM-(60°-∠BOM)=30°,
即∠BON-∠COM的度数是30°.
看了 如图1,点O为直线AB上一点...的网友还看了以下:
读我国某地的地形剖面图,回答以下各题。1.图中山脉②是我国下列哪一组重要的地理分界线2.对图示地区 2020-05-01 …
读《我国某地区图》,回答1~4题1、在上图a、b、c、d四条气温曲线中,能正确反映甲地气温年变化的 2020-05-15 …
(2009•长宁区二模)手t,曲线C:y=2x(0≤x≤2)两端分别为M、2,且2图⊥x轴于点图. 2020-05-15 …
读下图,完成1~2题。1、能正确反映华北地区土壤含盐量变化规律的曲线是[]A、甲曲线B、乙曲线C、 2020-05-15 …
如图,PC切⊙O于A,PO的延长线交⊙O于B,BC切⊙于点B.若CB:PC=1:2,求PO:OB的 2020-05-17 …
(2008•天门)如图,AB为⊙O的直径,C为⊙O上一点,∠BAC的平分线交⊙O于点D,过D点作E 2020-07-20 …
已知AB为⊙O的直径,C为⊙O上一点,D是BC的中点,过D作⊙O的切线交AC于E,DE=4,CE= 2020-07-20 …
我们把能够平分一个图形面积的直线叫“好线”,如图1.问题情境:如图2,M是圆O内的一定点,请在图2 2020-07-31 …
1.如图,△ABC在平面a外,AB∩a=P,BC∩a=Q,AC∩a=R,求证:P,Q,R三点共线. 2020-07-31 …
两道高中数学题向量OA,OB,OC为空间的一个基底.1.O,A,B,C四点不共线2.O,A,B,C四 2020-10-30 …