早教吧作业答案频道 -->数学-->
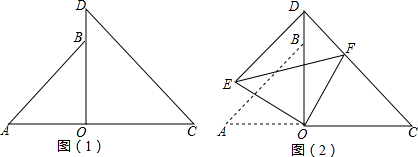
将两个大小不同的等腰直角三角形按如图(1)所示的方式放置,A,O,C在同一条直线上,O,B,D在同一条直线上,OA=OB,OC=OD.∠AOB=∠COD=90°,将等腰直角三角形AOB绕点O顺时针旋转(旋转角
题目详情
将两个大小不同的等腰直角三角形按如图(1)所示的方式放置,A,O,C在同一条直线上,O,B,D在同一条直线上,OA=OB,OC=OD.∠AOB=∠COD=90°,将等腰直角三角形AOB绕点O顺时针旋转(旋转角为α,0°<α<45°)得△EOF,使点B的对应点F落在CD边上,如图(2),连接ED,已知OD=2+2
,DF=2
,试解答下面问题:
(1)求证:DE2+DF2=EF2;
(2)求α的度数.(提示:在直角三角形中,一直角边的长等于斜边长的一半时,该直角边所对的角为30°)
| 3 |
| 2 |
(1)求证:DE2+DF2=EF2;
(2)求α的度数.(提示:在直角三角形中,一直角边的长等于斜边长的一半时,该直角边所对的角为30°)

▼优质解答
答案和解析
(1)∵OA=OB,OC=OD,∠AOB=∠COD=90°,
∴∠BAO=∠ODC=∠ABO=∠C=45°,
∵将等腰直角三角形AOB绕点O顺时针旋转(旋转角为α,0°<α<45°)得△EOF,
∴∠FEO=45°,
∴∠OEF=∠ODC,
∴D,E,F,O四点共圆,
∴∠EDF+∠EOF=180°,
∴∠EDF=90°,
∴DE2+DF2=EF2;
(2)∵OD=2+2
,
∴CD=2
+2
,
∵DF=2
,
∴CF=2
,
∵∠EOF=∠COD=90°,
∴∠DOE=∠FOC,
在△DOE与△COF中,
,
∴△DOE≌△COF,
∴DE=CF=2
,
∵tan∠DEF=
=
=
,
�
∴∠BAO=∠ODC=∠ABO=∠C=45°,
∵将等腰直角三角形AOB绕点O顺时针旋转(旋转角为α,0°<α<45°)得△EOF,
∴∠FEO=45°,
∴∠OEF=∠ODC,
∴D,E,F,O四点共圆,
∴∠EDF+∠EOF=180°,
∴∠EDF=90°,
∴DE2+DF2=EF2;
(2)∵OD=2+2
| 3 |
∴CD=2
| 2 |
| 6 |
∵DF=2
| 2 |
∴CF=2
| 6 |
∵∠EOF=∠COD=90°,
∴∠DOE=∠FOC,
在△DOE与△COF中,
|
∴△DOE≌△COF,
∴DE=CF=2
| 6 |
∵tan∠DEF=
| DF |
| DE |
2
| ||
2
|
| ||
| 3 |
�
看了 将两个大小不同的等腰直角三角...的网友还看了以下:
(1/3):1、一个圆的直径与一个正方形的边长相等,正方形的周长比圆多3.44厘米,圆的面积是(). 2020-03-31 …
平行线的判定方式 同位角平行,两直线…… 内错角平行,两直线…… 同胖内角互补,两直线…… 平行线 2020-05-13 …
长方形和正方形都有()条边,()个直角.长方形()边相等,正方形的四条边都().括号怎么填长方形和 2020-07-20 …
下列说法中正确的个数是()①同位角一定相等;②两边的平方和不等于第三边的平方的三角形不是直角三角形 2020-07-23 …
用放,靠,推,画的方法过直线外一点作已知直线的平行线的方法,依据是()A.内错角相等,两直线平行B 2020-07-23 …
如图,图中给出了过直线外一点作已知直线的平行线的方法,其依据的是()A.同位角相等,两直线平行B. 2020-07-23 …
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是()A.同位角相等,两直线平行B.内错角 2020-07-23 …
如图,三角形abc中ab等于ac,角bac等于90度,bc等于6,直线cm垂直于bc,在射线cb取 2020-07-25 …
在如图给出的过直线外一点作已知直线l1的平行线l2的方法,其依据是A.同位角相等,两直线平行;B. 2020-07-29 …
下列定理中有逆定理的个数是()①有两个角相等的三角形是等腰三角形;②在直接三角形中,斜边的平方等于 2020-08-01 …