早教吧作业答案频道 -->数学-->
如图1,∠AOB=α,∠COD=β,OM,ON分别是∠AOC,∠BOD的角平分线.(1)若∠AOB=50°,∠COD=30°,当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图2),则∠MON的大小为;(2)在(1)的
题目详情
如图1,∠AOB=α,∠COD=β,OM,ON分别是∠AOC,∠BOD的角平分线.
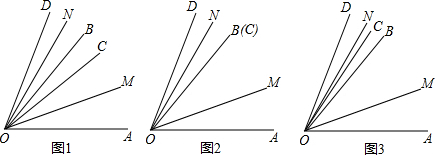
(1)若∠AOB=50°,∠COD=30°,当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图2),则∠MON的大小为___;
(2)在(1)的条件下,继续绕着点O逆时针旋转∠COD,当∠BOC=10°时(如图3),求∠MON的大小并说明理由;
(3)在∠COD绕点O逆时针旋转过程中,∠MON=___.(用含α,β的式子表示).
(1)若∠AOB=50°,∠COD=30°,当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图2),则∠MON的大小为___;
(2)在(1)的条件下,继续绕着点O逆时针旋转∠COD,当∠BOC=10°时(如图3),求∠MON的大小并说明理由;
(3)在∠COD绕点O逆时针旋转过程中,∠MON=___.(用含α,β的式子表示).

▼优质解答
答案和解析
 (1)如图2,∵OM,ON分别是∠AOC,∠BOD的角平分线,
(1)如图2,∵OM,ON分别是∠AOC,∠BOD的角平分线,
∴∠BOM=
∠AOB,∠BON=
∠BOD,
∴∠MON=
(∠AOB+∠BOD).
又∵∠AOB=50°,∠COD=30°,
∴∠MON=
(∠AOB+∠BOD)=
×(50°+30°)=40°.
故答案是:40°;
(2)如图3,∵∠BOD=∠BOC+∠COD=10°+30°=40°,ON平分∠BOD,
∴∠BON=
∠BOD=
×40°=20°.
∵∠AOC=∠BOC+∠AOB=10°+50°=60°,OM平分∠AOC,
∴∠COM=
∠AOC=
×60°=30°.
∴∠BOM=∠COM-∠BOC=30°-10°=20°.
∴∠MON=∠MOB+∠BON=20°+20°=40°;
(3)∵OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β,
∴∠MON=
α+
β=
(α+β);
故答案是:
 (1)如图2,∵OM,ON分别是∠AOC,∠BOD的角平分线,
(1)如图2,∵OM,ON分别是∠AOC,∠BOD的角平分线,∴∠BOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=
| 1 |
| 2 |
又∵∠AOB=50°,∠COD=30°,
∴∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:40°;
(2)如图3,∵∠BOD=∠BOC+∠COD=10°+30°=40°,ON平分∠BOD,
∴∠BON=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOC=∠BOC+∠AOB=10°+50°=60°,OM平分∠AOC,
∴∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOM=∠COM-∠BOC=30°-10°=20°.
∴∠MON=∠MOB+∠BON=20°+20°=40°;
(3)∵OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β,
∴∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:
| α+β |
| 2 |
看了 如图1,∠AOB=α,∠CO...的网友还看了以下:
满足{a}⊆M⊆{a,b,c,d}的集合M的个数是( ) 是{a} {a,b} {a,c} {a, 2020-04-05 …
已知a、b、c、d是非零实数,并满足a+b+c−dd=a+b−c+dc=a−b+c+db=−a+b 2020-05-13 …
英语单词辨音找出画()部分读音与其余不同的单词()1.A .kn(ee) B.n(e)ck C.r 2020-05-17 …
一个栈的入栈序列是a b c d e,则栈不可能的输出序列是( )。A.e d c b a B.d 2020-05-23 …
若a/b=c/d=e/f,则下列各式中正确的是().A.e/f=ac/bdB.e/f=(a+c+e 2020-06-06 …
初三比例式计算.如题.已知a/b=c/d(bd不等于0).判断下列比例式是否成立.并说明理由.a- 2020-06-10 …
设A=B=D=true,C=false,以下逻辑运算表达式值为真的有()。A.(A∧B)∨(C∧D 2020-07-18 …
公式难题,abcdefgn分别为不等的数值.a+b+n=?a+c+n=?a+d+n=?……………… 2020-08-04 …
公式难题...abcdefgn分别为不等的数值.a+b+n=?a+c+n=?a+d+n=?…………… 2020-11-28 …
分解因式(b+c-a-d)^4(b-c)(a-d)+(c+a-b-d)^4(c-a)(b-d)+(a 2021-01-04 …