早教吧作业答案频道 -->数学-->
问题情境将一副直角三角板(Rt△ABC和Rt△DEF)按图1所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量
题目详情
【问题情境】
将一副直角三角板(Rt△ABC和Rt△DEF)按图1所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由.
【探究展示】
小宇同学展示出如下正确的解法
OM=ON,
证明如下:
连接CO,则CO是AB边上的中线
∵CA=CB,
∴CO是∠ACB的角平分线.(依据1)
∵OM⊥AC,ON⊥BC,
∴OM=ON(依据2)
【反思交流】
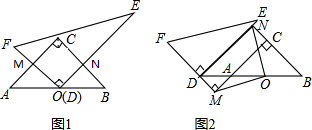
(1)上述证明过程中的“依据1”和“依据2”分别是指
依据1:___
依据2:___
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
【拓展延伸】
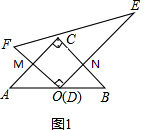
(3)将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM,ON,试判断线段OM,ON的数量关系与位置关系,并写出证明过程.
▼优质解答
答案和解析
 (1)
(1)
依据1:等腰三角形三线合一(或等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合);
依据2:角平分线上的点到角的两边距离相等.
(2)证明:∵CA=CB,
∴∠A=∠B,
∵O是AB的中点,
∴OA=OB.
∵DF⊥AC,DE⊥BC,
∴∠AMO=∠BNO=90°,
∵在△OMA和△ONB中
,
∴△OMA≌△ONB(AAS),
∴OM=ON.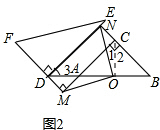
(3) OM=ON,OM⊥ON.
理由如下:
如图2,连接OC,
∵∠ACB=∠DNB,∠B=∠B,
∴△BCA∽△BND,
∴
=
,
∵AC=BC,
∴DN=NB.
∵∠ACB=90°,
∴∠NCM=90°=∠DNC,
∴MC∥DN,
又∵DF⊥AC,
∴∠DMC=90°,
即∠DMC=∠MCN=∠DNC=90°,
∴四边形DMCN是矩形,
∴DN=MC,
∵∠B=45°,∠DNB=90°,
∴∠3=∠B=45°,
∴DN=NB,
∴MC=NB,
∵∠ACB=90°,O为AB中点,AC=BC,
∴∠1=∠2=45°=∠B,OC=OB(斜边中线等于斜边一半),
在△MOC和△NOB中
,
∴△MOC≌△NOB(SAS),
∴OM=ON,∠MOC=∠NOB,
∴∠MOC-∠CON=∠NOB-∠CON,
即∠MON=∠BOC=90°,
∴OM⊥ON.
 (1)
(1) 依据1:等腰三角形三线合一(或等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合);
依据2:角平分线上的点到角的两边距离相等.
(2)证明:∵CA=CB,
∴∠A=∠B,
∵O是AB的中点,
∴OA=OB.
∵DF⊥AC,DE⊥BC,
∴∠AMO=∠BNO=90°,
∵在△OMA和△ONB中
|
∴△OMA≌△ONB(AAS),
∴OM=ON.

(3) OM=ON,OM⊥ON.
理由如下:
如图2,连接OC,
∵∠ACB=∠DNB,∠B=∠B,
∴△BCA∽△BND,
∴
| AC |
| DN |
| BC |
| BN |
∵AC=BC,
∴DN=NB.
∵∠ACB=90°,
∴∠NCM=90°=∠DNC,
∴MC∥DN,
又∵DF⊥AC,
∴∠DMC=90°,
即∠DMC=∠MCN=∠DNC=90°,
∴四边形DMCN是矩形,
∴DN=MC,
∵∠B=45°,∠DNB=90°,
∴∠3=∠B=45°,
∴DN=NB,
∴MC=NB,
∵∠ACB=90°,O为AB中点,AC=BC,
∴∠1=∠2=45°=∠B,OC=OB(斜边中线等于斜边一半),
在△MOC和△NOB中
|
∴△MOC≌△NOB(SAS),
∴OM=ON,∠MOC=∠NOB,
∴∠MOC-∠CON=∠NOB-∠CON,
即∠MON=∠BOC=90°,
∴OM⊥ON.
看了 问题情境将一副直角三角板(R...的网友还看了以下:
读下图,据此回答1-3题:1.四幅图中位在亚洲与北美洲边界的图是:A.a图B.b图C.c图D.d图 2020-05-02 …
下图为模拟膈肌运动的示意图,下列叙述正确的是()A.A图演示吸气,膈肌收缩B.B图演示吸气,膈肌舒 2020-05-02 …
二次函数y=ax²+bx+c的图像如图所示,若M=4a+2b+c,N=a-b+c,P=4a+2b, 2020-05-16 …
比例尺为1:100000的A图,将其比例尺放大到原来的4倍得到B图,B图的比例尺为(),B图的图幅 2020-07-16 …
1、将一图像文件A.BMP转换为B.JPG,再将B.JPG转换为C.BMP.则关于图像质量下列说法 2020-07-21 …
如图是气孔处于张开和闭合状态的示意图,下列有关叙述不正确的是()A.A图中①表示保卫细胞B.②是水 2020-07-22 …
二次函数y=ax2+bx+c的图象如图所示,根据图象可得a,b,c与0的大小关系是()A.a>0,b 2020-11-01 …
二次函数y=ax2+bx+c的图象如图所示,记p=|a-b+c|+|2a+b1、(2007湖北孝感) 2020-11-12 …
如图所示的电机模型中,属于交流发电机和直流发电机的分别是如()A.图(b)和图(a)B.图(c)和图 2020-12-13 …
(2009•静安区一模)在如图所描述的四副情景图中,研究方法相同的是()A.图(a)和图(c)B.图 2020-12-16 …