早教吧作业答案频道 -->物理-->
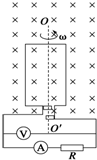
如图所示,线圈面积为0.05m2,共100匝,线圈总电阻为1Ω,与外电阻R=9Ω相连.当线圈在B=2πT的匀强磁场中绕OO′以转速n=300r/min匀速转动时,求:(1)若从线圈处于中性面开始计时,写出电动
题目详情
如图所示,线圈面积为0.05m2,共100匝,线圈总电阻为1Ω,与外电阻R=9Ω相连.当线圈在B=
T的匀强磁场中绕OO′以转速n=300r/min匀速转动时,求:
(1)若从线圈处于中性面开始计时,写出电动势的瞬时值表达式;
(2)两电表A、V的示数;
(3)线圈转过
s时,电动势的瞬时值;
(4)线圈转过
s的过程中,通过电阻R的电荷量;
(5)线圈匀速转一周外力做的功.
| 2 |
| π |

(1)若从线圈处于中性面开始计时,写出电动势的瞬时值表达式;
(2)两电表A、V的示数;
(3)线圈转过
| 1 |
| 60 |
(4)线圈转过
| 1 |
| 30 |
(5)线圈匀速转一周外力做的功.
▼优质解答
答案和解析
(1)线圈的角速度ω=2πn=10πrad/s,感应电动势的最大值Em=nBSω=100V,则从线圈处于中性面开始计时,电动势的瞬时值表达式为e=Emsinωt=100sin 10πtV
(2)电路中电流的有效值I=
,E=
Em,代入解得I=5
A,即电流表读数为5
A.
电压表读数为U=IR=45
V
(3)当线圈转过
s时,电动势的瞬时值e=100sin(10π×
) V=50 V.
(4)线圈转过t=
s的过程中,通过电阻R的电荷量为q=It=
×△t=
=
C.
(5)线圈匀速转一圈产生的总热量Q=I2(R+r)T=I2R•
=(5
)2×10×
=100 J.
答:
(1)若从线圈处于中性面开始计时,电动势的瞬时值表达式为100sin10πtV;
(2)电流表读数为5
A,电压表读数为45
V.
(3)当线圈转过
s时,电动势的瞬时值为50V;
(4)线圈转过180°的过程中,通过电阻的电荷量是
(1)线圈的角速度ω=2πn=10πrad/s,感应电动势的最大值Em=nBSω=100V,则从线圈处于中性面开始计时,电动势的瞬时值表达式为e=Emsinωt=100sin 10πtV
(2)电路中电流的有效值I=
| E |
| R+r |
| ||
| 2 |
| 2 |
| 2 |
电压表读数为U=IR=45
| 2 |
(3)当线圈转过
| 1 |
| 60 |
| 1 |
| 60 |
(4)线圈转过t=
| 1 |
| 30 |
| N△Φ |
| △t(R+r) |
| N△Φ |
| R+r |
| 1 |
| 2π |
(5)线圈匀速转一圈产生的总热量Q=I2(R+r)T=I2R•
| 2π |
| ω |
| 2 |
| 2π |
| 10π |
答:
(1)若从线圈处于中性面开始计时,电动势的瞬时值表达式为100sin10πtV;
(2)电流表读数为5
| 2 |
| 2 |
(3)当线圈转过
| 1 |
| 60 |
(4)线圈转过180°的过程中,通过电阻的电荷量是
看了 如图所示,线圈面积为0.05...的网友还看了以下:
设A为n阶矩阵,证明:R(A+I)+R(A-I)>=n已知R(A)=R(kA),k≠0;R(A+B 2020-05-14 …
设A为n(n>=2)阶方阵,证明当r(A)=n时,r(A*)=n当r(A)=2)阶方阵,证明当r( 2020-05-14 …
设A为n阶方阵,E为N阶单位矩阵,且A^2-A=2E,证明则r(2E-A)+r(E+A)=n设A为 2020-05-15 …
关于线性代数与几何分析的问题,请大家帮下忙~设A(-R^n*n,在欧氏空间R^n中,证明:=,其中 2020-06-27 …
设A为一个n阶方阵,证明r(A^n)=r(A^n+1)=r(A^n+2)不要用若当标准型,也不要证 2020-07-31 …
什么是二项式的通式?在二项式定理(a+b)^n=C(n,0)a^n+C(n,1)a^(n-1)b+ 2020-07-31 …
线性代数,基础解系设m*n矩阵A的秩r(A)=r,y1,y2.y(n-r+1)是非齐次线性方程组AX 2020-11-18 …
半径为r、电阻为R的n匝圆形线圈在边长为l的正方形abcd外,匀强磁场充满并垂直穿过该正方形区域,如 2021-01-13 …
半径为r、电阻为R的n匝圆形线圈在边长为l的正方形abcd之外,匀强磁场充满并垂直穿过该正方形区域, 2021-01-23 …
半径为r、电阻为R的n匝线圈在边长为l的正方形abcd之外,匀强磁场充满并垂直穿过该正方形区域,如图 2021-01-23 …
 扫描下载二维码
扫描下载二维码