如图，已知正方体ABCD-A1B1C1D1的棱长为4，点H在棱AA1上，且HA1=1，点E、F分别为B1C1、CC1的中点，P为侧面BCC1B1上一动点，且PE⊥PF，则当点P运动时，求HP2的最小值是（）A.9B.27-62C.51-142D.14

Question

如图，已知正方体ABCD-A₁B₁C₁D₁的棱长为4，点H在棱AA₁上，且HA₁=1，点E、F分别为B₁C₁、CC₁的中点，P为侧面BCC₁B₁上一动点，且PE⊥PF，则当点P运动时，求HP²的最小值是（　　）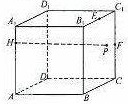

A. 9

B. 27-6

√(2)

C. 51-14

√(2)

D. 14-3

√(2)

Answer 1

以EF为直径在平面BCC₁B₁内做圆，该圆的半径为√(2)，再过H引BB₁的垂线，垂足为G，连接GP，
所以：HP²=HG²+GP²，其中HG为棱长等于4，因此当GP最小时，GP就取最小值：3-√(2)
所以：HP2=(3-√(2))2+42=27-6√(2)
则：HP²的最小值27-6√(2)
故选：B