已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B（点A在点B左侧），根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完

Question

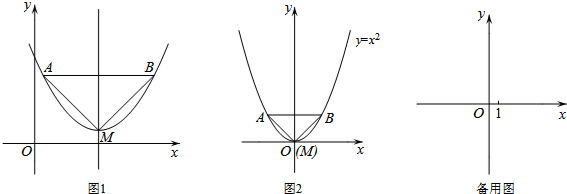
已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B（点A在点B左侧），根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”．
（1）①如图2，求出抛物线y=x²的“完美三角形”斜边AB的长；
②抛物线y=x²+1与y=x²的“完美三角形”的斜边长的数量关系是___；
（2）若抛物线y=ax²+4的“完美三角形”的斜边长为4，求a的值；
（3）若抛物线y=mx²+2x+n-5的“完美三角形”斜边长为n，且y=mx²+2x+n-5的最大值为-1，求m，n的值．

Answer 1

（1）①过点B作BN⊥x轴于N，如图2，

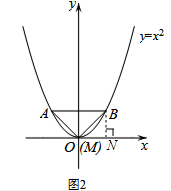
∵△AMB为等腰直角三角形，
∴∠ABM=45°，
∵AB∥x轴，
∴∠BMN=∠ABM=45°，
∴∠MBN=90°-45°=45°，
∴∠BMN=∠MBN，
∴MN=BN，
设B点坐标为（n，n），代入抛物线y=x²，
得n=n²，
∴n=1，n=0（舍去），
∴B（1，1）
∴MN=BN=1，
∴MB=√(12+12)=√(2)，
∴MA=MB=√(2)，
在Rt△AMB中，AB=√(MB2+MA2)=2，
∴抛物线y=x²的“完美三角形”的斜边AB=2．
②∵抛物线y=x²+1与y=x²的形状相同，
∴抛物线y=x²+1与y=x²的“完美三角形”的斜边长的数量关系是相等；
故答案为：相等．
（2）∵抛物线y=ax²与抛物线y=ax²+4的形状相同，
∴抛物线y=ax²与抛物线y=ax²+4的“完美三角形”全等，
∵抛物线y=ax²+4的“完美三角形”斜边的长为4，
∴抛物线y=ax²的“完美三角形”斜边的长为4，
∴B点坐标为（2，2）或（2，-2），
把点B代入y=ax²中，
∴a=±(1)/(2)．
（3）∵y=mx²+2x+n-5的最大值为-1，
∴(4m(n-5)-4)/(4m)=-1，
∴mn-4m-1=0，
∵抛物线y=mx²+2x+n-5的“完美三角形”斜边长为n，
∴抛物线y=mx²的“完美三角形”斜边长为n，
∴B点坐标为((n)/(2)，-(n)/(2))，
∴代入抛物线y=mx²，得((n)/(2))2•m=-(n)/(2)，
∴mn=-2或n=0（不合题意舍去），
∴m=-(3)/(4)，
∴n=(8)/(3)．