早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=mx(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).(1)求反比例函数和一次函数的解析式;(2
题目详情
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=
(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).
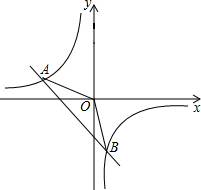
(1)求反比例函数和一次函数的解析式;
(2)连接OA,OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
| m |
| x |

(1)求反比例函数和一次函数的解析式;
(2)连接OA,OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
▼优质解答
答案和解析
(1)∵反比例函数y2=
(m为常数,且m≠0)的图象过点A(-2,1),
∴m=-2×1=-2,
∴反比例函数解析式为y2=-
;
∵点B(1,n)在反比例函数y2=-
的图象上,
∴n=-2,即点B(1,-2).
将点A(-2,1)、B(1,-2)代入到y1=ax+b(a,b为常数,且a≠0)中,
得:
,解得:
,
∴一次函数解析式为y1=-x-1.
(2)令y1=-x-1中x=0,则y=-1,
∴点C(0,-1),OC=1.
∴S△AOB=
OC•(xB-xA)=
×1×[1-(-2)]=
.
(3)观察函数图象,发现:
在x轴的下方,当x>1时,一次函数图象在反比例函数图形的下方,
∴当y1<y2<0时,自变量x的取值范围为x>1.
| m |
| x |
∴m=-2×1=-2,
∴反比例函数解析式为y2=-
| 2 |
| x |
∵点B(1,n)在反比例函数y2=-
| 2 |
| x |
∴n=-2,即点B(1,-2).
将点A(-2,1)、B(1,-2)代入到y1=ax+b(a,b为常数,且a≠0)中,

得:
|
|
∴一次函数解析式为y1=-x-1.
(2)令y1=-x-1中x=0,则y=-1,
∴点C(0,-1),OC=1.
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(3)观察函数图象,发现:
在x轴的下方,当x>1时,一次函数图象在反比例函数图形的下方,
∴当y1<y2<0时,自变量x的取值范围为x>1.
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
1.函数y=(a-3)x+b+2经过点(-1,2)和(0,0)求a.b及函数解析式2.已知正比例函 2020-04-27 …
根号x反导数 2020-06-13 …
关于反比例函数反比例的区别y与x-1成反比例.当x=时y=时求y与x的函数关系y=2/x-1问:1 2020-06-13 …
1.已知Y与X成反比例,且当X=-1时,Y=2,写出Y与X的函数关系式 2.反比例函数Y=3X分之 2020-06-27 …
初二旳几道数学题.1.已知y=y1+y2,y1与x成正比例,y2与x^2成反比例,且x=2与x=3 2020-06-29 …
y=φ(x)为二阶可导函数f(x)反函数,f(x)的n次方大于零,则y=φ(x)为——答...y= 2020-07-29 …
反比例函数22.已知变量y-1与x成反比例,且当x=2时y=9(1)写出y与x之间的函数解析式;( 2020-08-03 …
原函数积分加反函数积分…我总不可能画个图吧…怎办…原函数f(x)在[a,b]上单调递增,a>0,f( 2020-11-08 …
谁能证明这个概率论命题概率分布函数F(x),反函数为FInv(y),如果y是[0,1]区间的均匀分布 2020-12-13 …
高等数学求导已知y=f(x)的导数f'(x)=(-1-2x)/(1+x+x2)2分母是一加x再加x方 2021-01-23 …