早教吧作业答案频道 -->数学-->
如图,已知直线y=3x+3与x轴交于点A,与y轴交于点C,过点C的直线y=-x+b与x轴交于点B.(1)b的值为;(2)若点D的坐标为(0,-1),将△BCD沿直线BC对折后,点D落到第一象限的点E处,求证:
题目详情
如图,已知直线y=3x+3与x轴交于点A,与y轴交于点C,过点C的直线y=-x+b与x轴交于点B.
(1)b的值为___;
(2)若点D的坐标为(0,-1),将△BCD沿直线BC对折后,点D落到第一象限的点E处,求证:四边形ABEC是平行四边形;
(3)在直线BC上是否存在点P,使得以P、A、D、B为顶点的四边形是平行四边形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
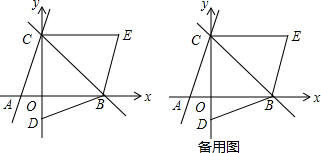
(1)b的值为___;
(2)若点D的坐标为(0,-1),将△BCD沿直线BC对折后,点D落到第一象限的点E处,求证:四边形ABEC是平行四边形;
(3)在直线BC上是否存在点P,使得以P、A、D、B为顶点的四边形是平行四边形?如果存在,请求出点P的坐标;如果不存在,请说明理由.

▼优质解答
答案和解析
(1)∵直线y=3x+3与x轴交于点A,与y轴交于点C,
∴C(0,3),
∵过点C的直线y=-x+b与x轴交于点B,
∴b=3,
故答案为3,
(2)证明:当b=3时,直线BC为y=-x+3
由x=0得,y=3,
∴C(0,3),OC=3
由y=0得,x=3,
∴B(3,0),OB=3
∴OB=OC=3
∴∠OBC=∠OCB=45°
由折叠得:∠BCE=∠OCB=45°
CE=CD=OC+OD=4
∴∠OBC=∠BCE
∴CE∥AB
由y=3x+3,令y=0得,x=-1,
∴A(-1,0)
∴AB=OA+OB=3+1=4
∴AB=CE
∴四边形ABEC为平行四边形.
(3) 存在点P,使以P、A、D、B为顶点的四边形是平行四边形.
方法①如图,
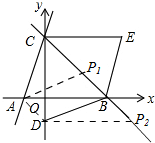
∵A(-1,0)、D(0,-1),
∴直线AD解析式为y=-x-1,
∵B(3,0),C(0,3),
∴直线BC解析式为y=-x+3.
∴AD∥BC,
∵点P在直线BC上,
∴设点P坐标为(m,-m+3),
∴PB2=(m-3)2+(-m+3)2,
∵使得以P、A、D、B为顶点的四边形是平行四边形,
∴PB=AD,
∴PB2=AD2,
∵AD2=2,
∴(m-3)2+(-m+3)2=2.
∴m1=2,m2=4,
∴P(2,1)或P(4,-1),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.点P的坐标为P1(2,1)或P2(4,-1).
方法②∵A(-1,0)、D(0,-1),
∴直线AD解析式为y=-x-1,
∵B(3,0),
∴过点B的直线l∥AD,直线l解析式为y=-x+3,
∴D(0,-1),
∴过点D的直线l'∥AB,直线l'的解析式为y=-1,
∴直线l和l'的交点坐标为M(4,-1),
∵直线BC解析式为y=-x+3.
∴点M在直线BC上,即点M就是所找的点P,
∴P(4,-1),
∵D(0,-1),B(3,0),
∴直线BD的解析式为y=
x-1,
∴过点A的直线a∥BD,直线a的解析式为y=
x+
,
∵直线l解析式为y=-x+3,
∴直线l和直线a的交点坐标为N(2,1),
∵直线BC解析式为y=-x+3.
∴点N在直线BC上,即点N就是所找的点P,
∴P(2,1),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.点P的坐标为P1(2,1)或P2(4,-1).
∴C(0,3),
∵过点C的直线y=-x+b与x轴交于点B,
∴b=3,
故答案为3,
(2)证明:当b=3时,直线BC为y=-x+3
由x=0得,y=3,
∴C(0,3),OC=3
由y=0得,x=3,
∴B(3,0),OB=3
∴OB=OC=3
∴∠OBC=∠OCB=45°
由折叠得:∠BCE=∠OCB=45°
CE=CD=OC+OD=4
∴∠OBC=∠BCE
∴CE∥AB
由y=3x+3,令y=0得,x=-1,
∴A(-1,0)
∴AB=OA+OB=3+1=4
∴AB=CE
∴四边形ABEC为平行四边形.
(3) 存在点P,使以P、A、D、B为顶点的四边形是平行四边形.
方法①如图,

∵A(-1,0)、D(0,-1),
∴直线AD解析式为y=-x-1,
∵B(3,0),C(0,3),
∴直线BC解析式为y=-x+3.
∴AD∥BC,
∵点P在直线BC上,
∴设点P坐标为(m,-m+3),
∴PB2=(m-3)2+(-m+3)2,
∵使得以P、A、D、B为顶点的四边形是平行四边形,
∴PB=AD,
∴PB2=AD2,
∵AD2=2,
∴(m-3)2+(-m+3)2=2.
∴m1=2,m2=4,
∴P(2,1)或P(4,-1),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.点P的坐标为P1(2,1)或P2(4,-1).
方法②∵A(-1,0)、D(0,-1),
∴直线AD解析式为y=-x-1,
∵B(3,0),
∴过点B的直线l∥AD,直线l解析式为y=-x+3,
∴D(0,-1),
∴过点D的直线l'∥AB,直线l'的解析式为y=-1,
∴直线l和l'的交点坐标为M(4,-1),
∵直线BC解析式为y=-x+3.
∴点M在直线BC上,即点M就是所找的点P,
∴P(4,-1),
∵D(0,-1),B(3,0),
∴直线BD的解析式为y=
| 1 |
| 3 |
∴过点A的直线a∥BD,直线a的解析式为y=
| 1 |
| 3 |
| 1 |
| 3 |
∵直线l解析式为y=-x+3,
∴直线l和直线a的交点坐标为N(2,1),
∵直线BC解析式为y=-x+3.
∴点N在直线BC上,即点N就是所找的点P,
∴P(2,1),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.点P的坐标为P1(2,1)或P2(4,-1).
看了 如图,已知直线y=3x+3与...的网友还看了以下:
英语翻译1.明天我去看奶奶2.明年我们将要搬到北京3.3年后他将成为一名医生4.下个假期我要学做饭 2020-05-15 …
已知函数f(x)=2√3cos^x-2sinxcosx-√3(1)求函数的单调递减区间(2)若将函 2020-05-15 …
过来看看,任取一个自然数,将其个位上的数字求和,再将这个和乘以3后加上1,得到一个新的自然数;再将 2020-05-17 …
王先生看到银行公布的存款利率如下表所示:王先生3年后即将退休,他准备现在就将一笔钱存入银行3年王先 2020-06-02 …
1.小林喝了一本牛奶的1/3后到满水,最后全部喝完.小林喝的牛奶多还是谁多?2.护林员叔叔有一辆三 2020-07-01 …
将2000元,存定期3年,到期后连本带利再转存3年,到期后,将得到本息共多少元?存期/1年/2年/ 2020-07-23 …
有如下算法描述①输入整数a②如果a是奇数转到⑥③如果a是偶数转到⑤④将a的值相乘以后赋给a⑤将a的 2020-07-24 …
钢铁雄心2指挥上限到底怎么算的最后举个例子,ABCDE五个连续相邻的省共同与F接壤,假设进攻兵力为: 2020-11-13 …
英语翻译1飞机几点起飞?/几点降落?2火车几点发车?/几点到站?3飞机将在20分钟后起飞/降落4火车 2020-12-23 …
1.小林喝了一本牛奶的1/3后到满水,最后全部喝完.小林喝的牛奶多还是谁多?2.护林员叔叔有一辆三轮 2020-12-24 …