如图1，将两个等腰三角形ABC和DEC拼合在一起，其中∠C=90°，AC=BC，CD=CE．（1）操作发现如图2，固定△ABC，把△DEC绕着顶点C旋转，使点D落在BC边上．填空：线段AD与BE的关系是①位置关系：

Question

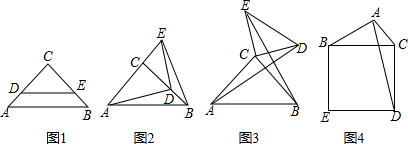
如图1，将两个等腰三角形ABC和DEC拼合在一起，其中∠C=90°，AC=BC，CD=CE．
（1）操作发现
如图2，固定△ABC，把△DEC绕着顶点C旋转，使点D落在BC边上．
填空：线段AD与BE的关系是
①位置关系：___
②数量关系：___
（2）变式探究
当△DEC绕点C旋转到图3的位置时，（1）中的结论还成立吗？请说明理由；
（3）解决问题
如图4，已知线段AB=5，线段AC=2 √(2)，以BC为边作一个正方形BCDE，连接AD，随着边BC的变化，线段AD的长也会发生变化．请直接写出线段AD的取值范围．

Answer 1

（1）延长AD交BE于点F．

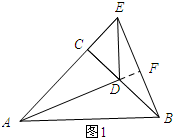
在△ACD和△BCE中，

CD=CE

∠ACD=∠ECB=90°

AC=BC

，
∴△ACD≌△BCE．
∴AD=BE，∠CAD=∠CBE．
又∵∠CDA=∠FDB，
∴∠DFB=∠DCA=90°．
∴AD⊥BE．
故答案为：AD⊥BE，AD=BE．
（2）如图2所示：记AD与BC的交点为O，BE与AD的交点为F．

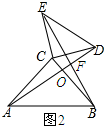
∵∠ACB=∠ECD=90°，
∴∠ACB+∠BCD=∠ECD+∠BCD，即∠ACD=∠BCE．
在△ACD和△BCE中，

AC=BC

∠ACD=∠BCE

CD=CE

，
∴△ACD≌△BCE．
∴AD=BE，∠CAD=∠CBE．
又∵∠AOC=∠BOF，
∴∠ACO=∠BFO=90°．
∴AD⊥BE．
（3）如图3所示：过点C作CE⊥AC，取AC=CE，连结BE．

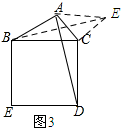
∵AC=CE=2√(2)，∠ACE=90°，
∴AE=4．
∵AE=4，AB=5，
∴1<BE<9．
∵∠DCB=∠ACE=90°，
∴∠DCB+∠BCA=∠BCA+∠ACE，即∠ACD=∠BCE．
在△BCE和△DCA中

AC=CE

∠BCE=∠ACD

BC=CD

，
∴△BCE≌△DCA．
∴AD=BE．
∴1<AD<9．