早教吧作业答案频道 -->数学-->
已知∠AOB=100°,射线OC在∠AOB的内部,射线OE,OF分别是∠AOC和∠COB的角平分线.(1)如图1,若∠AOC=30°,求∠EOF的度数;(2)请从下面A,B两题中任选一题作答,我选择题.A.如图2
题目详情
已知∠AOB=100°,射线OC在∠AOB的内部,射线OE,OF分别是∠AOC和∠COB的角平分线.
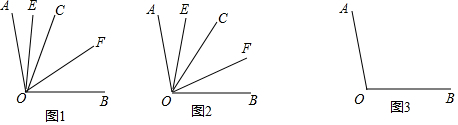
(1)如图1,若∠AOC=30°,求∠EOF的度数;
(2)请从下面A,B两题中任选一题作答,我选择___题.
A.如图2,若射线OC在∠AOB的内部绕点O旋转,则∠EOF的度数为___.
B.若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC、∠BOC均是指小于180°的角),其余条件不变,请借助图3探究∠EOF的大小,直接写出∠EOF的度数.

(1)如图1,若∠AOC=30°,求∠EOF的度数;
(2)请从下面A,B两题中任选一题作答,我选择___题.
A.如图2,若射线OC在∠AOB的内部绕点O旋转,则∠EOF的度数为___.
B.若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC、∠BOC均是指小于180°的角),其余条件不变,请借助图3探究∠EOF的大小,直接写出∠EOF的度数.
▼优质解答
答案和解析
(1)∵∠AOB=100°,∠AOC=30°,
∴∠BOC=∠AOB-∠AOC=70°,
∵OE,OF分别是∠AOC和∠COB的角平分线,
∴∠EOC=
∠AOC=15°,∠FOC=
∠BOC=35°,
∴∠EOF=∠EOC+∠FOC=15°+35°=50°;
(2)A.∵OE,OF分别是∠AOC和∠COB的角平分线,
∴∠EOC=
∠AOC,∠FOC=
∠BOC,
∴∠EOF=∠EOC+∠FOC=
∠AOB=
×100°=50°;
B.①射线OE,OF只有1个在∠AOB外面,如图3①,
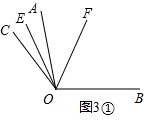
∠EOF=∠FOC-∠COE=
∠BOC-
∠AOC=
(∠BOC-∠AOC)=
∠AOB=
×100°=50°.
②射线OE,OF2个都在∠AOB外面,如图3②,
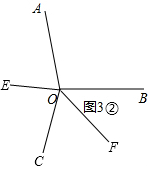
∠EOF=∠EOC+∠COF=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
(360°-∠AOB)=
×260°=130°.
故∠EOF的度数是50°或130°.
故答案为:A,50°.
∴∠BOC=∠AOB-∠AOC=70°,
∵OE,OF分别是∠AOC和∠COB的角平分线,
∴∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=∠EOC+∠FOC=15°+35°=50°;
(2)A.∵OE,OF分别是∠AOC和∠COB的角平分线,
∴∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=∠EOC+∠FOC=
| 1 |
| 2 |
| 1 |
| 2 |
B.①射线OE,OF只有1个在∠AOB外面,如图3①,

∠EOF=∠FOC-∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②射线OE,OF2个都在∠AOB外面,如图3②,

∠EOF=∠EOC+∠COF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故∠EOF的度数是50°或130°.
故答案为:A,50°.
看了 已知∠AOB=100°,射线...的网友还看了以下:
a=xa+a=a+x2a=a+x2a-2x=a+x-2x2(a-x)=a-x2=1到底a=xa+a= 2020-03-30 …
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
(a的平方-2+a的负二次方)÷(a的平方-a的负二次方) 化简.第一步 原式=(a-a^-1)² 2020-04-05 …
采购员用一张1万元支票去购物.购单价为590元的A种物品若干件,又购单价为670元的B种物品若干件 2020-04-07 …
1.(a^2+3)(a-2)-a(a^2-2a-2)=?2.(3/5a^5b^3+9/5a^7b^ 2020-04-27 …
曲线是指指数函数y=a的x次方,已知a的取值为根号2,三分之四,十分之三,五分之一,则曲线C1C2 2020-05-12 …
线性代数题:设A为n阶方阵,A*是A的伴随矩阵,如果/A/=a≠0,则/A*/=()设A为n阶方阵 2020-05-15 …
质量a的A物质,b的B物质充分反应,生成的c为什么小于等于(a+b)?可以小于吗?A+B----C 2020-05-21 …
(非诚心答题的,请绕道)已知集合A={x│x²+px+q=0},B={x│2x²-7x+3=0}, 2020-05-21 …