早教吧作业答案频道 -->数学-->
若一个凸四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫做这个四边形的“等腰线”.(1)如图,在四边形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC,请找出
题目详情
若一个凸四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫做这个四边形的“等腰线”.
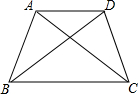
(1)如图,在四边形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC,请找出图中的“等腰线”,并说明理由;
(2)四边形ABCD中,AD=AB=BC,∠BAD=90°,AC是四边形ABCD的“等腰线”,求∠BCD的度数.

(1)如图,在四边形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC,请找出图中的“等腰线”,并说明理由;
(2)四边形ABCD中,AD=AB=BC,∠BAD=90°,AC是四边形ABCD的“等腰线”,求∠BCD的度数.
▼优质解答
答案和解析
(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADB=∠DBC.
∵∠BAD=120°,
∴∠ABC=60°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠ABD=∠ADB,
∴△ADB是等腰三角形.
在△BCD中,∠C=75°,∠DBC=30°,
∴∠BDC=∠C=75°,
∴△BCD为等腰三角形,
∴BD是梯形ABCD的和谐线;
(2)∵AC是四边形ABCD的和谐线,
∴△ACD是等腰三角形.
∵AB=AD=BC,
如图4,当AD=AC时,
∴AB=AC=BC,∠ACD=∠ADC
∴△ABC是正三角形,
∴∠BAC=∠BCA=60°.
∵∠BAD=90°,
∴∠CAD=30°,
∴∠ACD=∠ADC=75°,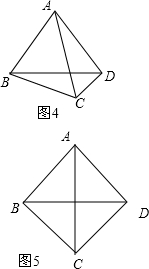
∴∠BCD=60°+75°=135°.
如图5,当AD=CD时,
∴AB=AD=BC=CD.
∵∠BAD=90°,
∴四边形ABCD是正方形,
∴∠BCD=90°
如图6,当AC=CD时,过点C作CE⊥AD于E,过点B作BF⊥CE于F,
∵AC=CD.CE⊥AD,
∴AE=
AD,∠ACE=∠DCE.
∵∠BAD=∠AEF=∠BFE=90°,
∴四边形ABFE是矩形.
∴BF=AE.
∵AB=AD=BC,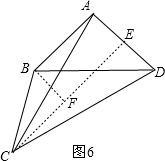
∴BF=
BC,
∴∠BCF=30°.
∵AB=BC,
∴∠ACB=∠BAC.
∵AB∥CE,
∴∠BAC=∠ACE,
∴∠ACB=∠ACE=
∠BCF=15°,
∴∠BCD=15°×3=45°.
∴∠ABC+∠BAD=180°,∠ADB=∠DBC.
∵∠BAD=120°,
∴∠ABC=60°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠ABD=∠ADB,
∴△ADB是等腰三角形.
在△BCD中,∠C=75°,∠DBC=30°,
∴∠BDC=∠C=75°,
∴△BCD为等腰三角形,
∴BD是梯形ABCD的和谐线;
(2)∵AC是四边形ABCD的和谐线,
∴△ACD是等腰三角形.
∵AB=AD=BC,
如图4,当AD=AC时,
∴AB=AC=BC,∠ACD=∠ADC
∴△ABC是正三角形,
∴∠BAC=∠BCA=60°.
∵∠BAD=90°,
∴∠CAD=30°,
∴∠ACD=∠ADC=75°,

∴∠BCD=60°+75°=135°.
如图5,当AD=CD时,
∴AB=AD=BC=CD.
∵∠BAD=90°,
∴四边形ABCD是正方形,
∴∠BCD=90°
如图6,当AC=CD时,过点C作CE⊥AD于E,过点B作BF⊥CE于F,
∵AC=CD.CE⊥AD,
∴AE=
| 1 |
| 2 |
∵∠BAD=∠AEF=∠BFE=90°,
∴四边形ABFE是矩形.
∴BF=AE.
∵AB=AD=BC,

∴BF=
| 1 |
| 2 |
∴∠BCF=30°.
∵AB=BC,
∴∠ACB=∠BAC.
∵AB∥CE,
∴∠BAC=∠ACE,
∴∠ACB=∠ACE=
| 1 |
| 2 |
∴∠BCD=15°×3=45°.
看了 若一个凸四边形的一条对角线把...的网友还看了以下:
下面试题:11111111111对于化学反应A+B=C+D的下列说法中,正确的是()A.若A、B、 2020-04-27 …
关于化学反应A+B=C+D,下列说法中正确的是A.若生成物C和D分别是盐和水,则反应物一定是酸和碱 2020-05-13 …
已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧CA分为三等份,连接MC并延长交y轴于 2020-05-14 …
已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧CA分为三等份,连接MC并延长交y轴于 2020-05-14 …
已知│a│=3,│b│=2,a与b的夹角为60度,c=3a+5b,d=ma-b.若c⊥d,求m的值 2020-05-16 …
若ab互为相反数a不等于0,则关于x的方程ax+b=0的解是( ) 下列说法中正确 是 若a若ab 2020-05-16 …
用复合命题推理的有关知识解答下列问题:已知:①A真包含于B②有C不是B③若C不真包含A,则C真包含 2020-06-14 …
(2013•永春县模拟)已知A、B为单质,C为化合物.能实现下述转化关系的是()A+B点燃C溶于水 2020-07-16 …
如图a、b、c表示现代工程技术,①②③表示对应结果,下列说法正确的是()A.若b是体外受精,则可发挥 2020-11-02 …
如图为人体某处的血管及血液情况示意图,叙述正确的是()A.若c处氧气含量降低,则b处为肺泡外的毛细血 2020-11-04 …