已知关于x的方程x2+（a+1）x+a+b+1=0的两个根分别为α，β，其中α∈（0，1），β∈（1，+∞），则b-1a+1的取值范围是（）A.（-2，0）B.（0，2）C.（-1，0）D.（0，1）

Question

已知关于x的方程x²+（a+1）x+a+b+1=0的两个根分别为α，β，其中α∈（0，1），β∈（1，+∞），则

(b-1)/(a+1)的取值范围是（　　）

A. （-2，0）

B. （0，2）

C. （-1，0）

D. （0，1）

Answer 1

设f（x）=x²+（a+1）x+a+b+1，
则α，β是f（x）=0的零点，
∵α∈（0，1），β∈（1，+∞），
∴f（0）>0，f（1）<0，α+β=-（a+1）>0，αβ=a+b+1>0，
即

a+b+1>0

2a+b+3<0

-a-1>0

，作出平面区域如图：
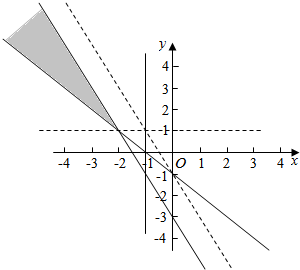
由图象可知，当过（-1，1）的直线平行于2a+b+3=0时，斜率最小为-2，
过（-1，1）的直线与x轴平行时，斜率最大为0．
故选A．