早教吧作业答案频道 -->数学-->
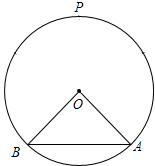
如图,圆O的半径为2,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧AB的中点,设C,D(C在D左侧)为优弧AB上的两个不同的动点,且CD∥BA,记∠POD=α,四边形ABCD的面积为S.(1)求S关于α的
题目详情
如图,圆O的半径为
,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧AB的中点,设C,D(C在D左侧)为优弧AB上的两个不同的动点,且CD∥BA,记∠POD=α,四边形ABCD的面积为S.
(1)求S关于α的函数关系;
(2)当α为何值时,S取得最大值?并求出S的最大值.
| 2 |

(1)求S关于α的函数关系;
(2)当α为何值时,S取得最大值?并求出S的最大值.
▼优质解答
答案和解析
(1)如下图所示:
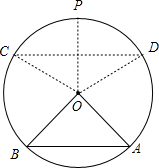
∵圆O的半径为
,A,B为圆O上的两个定点,且∠AOB=90°,
∴AB=
=2,O到AB的距离d=1,
若∠POD=α,则CD=2
sinα,O到CD的距离h=
cosα,
故S=
(2
sinα+2)(
cosα+1)=2sinαcosα+
(sinα+cosα)+1=(sinα+cosα)2+
(sinα+cosα)=2sin2(α+
)+2sin(α+
).
(2)令t=sin(α+
).则S=2t2+2t,t∈[
,1],
∵S=2t2+2t的图象是开口朝上,且以直线t=-
为对称的抛物线,
故当t=1,即α=

∵圆O的半径为
| 2 |
∴AB=
| OB2+OA2 |
若∠POD=α,则CD=2
| 2 |
| 2 |
故S=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
(2)令t=sin(α+
| π |
| 4 |
| ||
| 2 |
∵S=2t2+2t的图象是开口朝上,且以直线t=-
| 1 |
| 2 |
故当t=1,即α=
| π |
| 4 |
看了 如图,圆O的半径为2,A,B...的网友还看了以下:
选择正确读音。1.结束[]A.ji6s)B.ji5sh)C.ji6sh)2.立即[]A.l@j@B 2020-05-13 …
设ab是两条异面直线,P是ab外的一点,则下列结论正确的是()A.过P有一条直线和ab都平行B.过 2020-05-13 …
pgA·nH2O受热失去全部结晶水后,质量为qg,由此可以得知该结晶水合物的化学式量为[]A.18 2020-05-13 …
pgA·nH2O受热pgA·nH2O受热失去全部结晶水后,质量为qg,由此可以得知该结晶水合物的化 2020-05-13 …
(ab)的p次方=,(b分之a)的p次方=,其中a>0,b>0,p为有理数 2020-05-13 …
去年产量比前年产量增长p%,则前年产量比去年产量下降的比率是()A.100p100+p%B.p10 2020-05-13 …
(09西安一中第一次月考)图中的图P和图Q为处于不同分裂时期的两种动物细胞,都含有两对同源染色体。 2020-05-14 …
(2014•崇明县二模)在⊙O中,圆心O在坐标原点上,半径为210,点P的坐标为(4,个),那么点 2020-05-17 …
(2014•湖南模拟)定义全集U的子集P的特征函数fP(x)=1,x∈P0,x∈∁UP,这里∁UP 2020-05-24 …
设X1,X2,…,Xn,…为独立同分布的随机变量列,且均服从参数为λ(λ>1)的指数分布,记Φ(x 2020-06-10 …
 扫描下载二维码
扫描下载二维码
