早教吧作业答案频道 -->数学-->
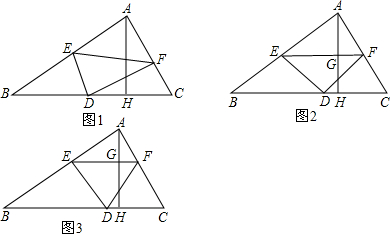
在△ABC中,BC=8,高AH为4,△DEF在△ABC内,三个顶点D、E、F分别在BC、AB和AC上,且点D与点A在直线EF的异侧,我们称△DEF为△ABC的内接三角形.(1)如图1,当△DEF∽△ABC,且EF=3时,求△DEF的
题目详情
在△ABC中,BC=8,高AH为4,△DEF在△ABC内,三个顶点D、E、F分别在BC、AB和AC上,且点D与点A在直线EF的异侧,我们称△DEF为△ABC的内接三角形.
(1)如图1,当△DEF∽△ABC,且EF=3时,求△DEF的面积;
(2)如图2,在△ABC的内接△DEF中,DE=DF,∠EDF=90°,且EF∥BC,EF与AH交于G点,求△DEF的面积;
(3)如图3,在△ABC的内接三角形DEF中,DE=DF,且EF∥BC,EF与AH交于G点,求等腰△DEF面积的最大值.
(1)如图1,当△DEF∽△ABC,且EF=3时,求△DEF的面积;
(2)如图2,在△ABC的内接△DEF中,DE=DF,∠EDF=90°,且EF∥BC,EF与AH交于G点,求△DEF的面积;
(3)如图3,在△ABC的内接三角形DEF中,DE=DF,且EF∥BC,EF与AH交于G点,求等腰△DEF面积的最大值.

▼优质解答
答案和解析
 (1)∵BC=8,高AH为4,
(1)∵BC=8,高AH为4,
∴△ABC的面积为
×8×4=16,
∵△DEF∽△ABC,
∴
=(
)2,
∴△DEF的面积为:
;
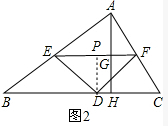
(2)如图2,作DP⊥EF于P,
∵DE=DF,∠EDF=90°,
∴PD=
EF,
由题意可知,四边形PDHG为矩形,∴PD=GH,
设EF=x,则PD=GH=
x,
∵EF∥BC,
∴
=
,即
=
,
解得,x=4,
∴△DEF的面积=
×EF×PD=4;
(3)如图2,设EF=a,
∵EF∥BC,
∴
=
,即
=
,
解得,GH=4-
a,
∵PD=GH,
∴△DEF面积=
×a×(4-
a)=-
(a-4)2+4,
∵-
<0,
∴等腰△DEF面积的最大值为4.
 (1)∵BC=8,高AH为4,
(1)∵BC=8,高AH为4,∴△ABC的面积为
| 1 |
| 2 |
∵△DEF∽△ABC,
∴
| △DEF的面积 |
| △ABC的面积 |
| EF |
| BC |
∴△DEF的面积为:
| 9 |
| 4 |
(2)如图2,作DP⊥EF于P,
∵DE=DF,∠EDF=90°,
∴PD=
| 1 |
| 2 |
由题意可知,四边形PDHG为矩形,∴PD=GH,
设EF=x,则PD=GH=
| 1 |
| 2 |
∵EF∥BC,
∴
| EF |
| BC |
| AG |
| AH |
| x |
| 8 |
4-
| ||
| 4 |
解得,x=4,
∴△DEF的面积=
| 1 |
| 2 |
(3)如图2,设EF=a,
∵EF∥BC,
∴
| EF |
| BC |
| AG |
| AH |
| a |
| 8 |
| 4-GH |
| 4 |
解得,GH=4-
| 1 |
| 2 |
∵PD=GH,
∴△DEF面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵-
| 1 |
| 2 |
∴等腰△DEF面积的最大值为4.
看了 在△ABC中,BC=8,高A...的网友还看了以下:
英语中不送气音的问题英语里的不送气音比如[b]发这个音时候不要屏住气发[b]吗?还是尽量不要吐起气 2020-04-08 …
如果向量a,b,c共面,b,c,d也共面,那么a,b,c,d是否共面?如果不一定共面,请举例说明浪 2020-05-13 …
如图,△ABC≌△A'B'C',AD,A'D'分别是△ABC,△A'B'C'的对应边上的中线.AD 2020-05-16 …
在一张四边形纸片ABCD中,∠B=∠D=90度,把纸片按如图所示的方式折叠,使点B落在AD边上的点 2020-05-16 …
一张四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的点B'处,A 2020-05-16 …
如图,在四边形纸片ABCD中,∠B=∠D=90°,把纸片按如图虚线折叠,使点B落在AD边上的点B‘ 2020-05-16 …
如图,某海滨浴场的海岸线可以看作直线,如图,1号救生员在岸边的点A看到海中的点B有人求救,便立即向 2020-05-16 …
如图,将矩形纸片ABCD按如下的顺序进行折叠:对折,展平,得折痕EF(如图①);沿CG折叠,使点B 2020-05-17 …
如a如b式成语如:如醉如痴 2020-05-17 …
如果把分式a+b/a中的a,b都变为原来的1/2,那么分式的值会不会改变?如果是分式a+b/a·a 2020-05-22 …