早教吧作业答案频道 -->数学-->
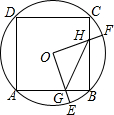
如图,边长为4的正方形ABCD内接于点O,点E是AB上的一动点(不与A、B重合),点F是BC上的一点,连接OE、OF,分别与AB、BC交于点
题目详情
如图,边长为4的正方形ABCD内接于点O,点E是
上的一动点(不与A、B重合),点F是
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
①
=
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+
.
其中正确的是___(把你认为正确结论的序号都填上).
 |
| AB |
 |
| BC |
①
 |
| AE |
 |
| BF |
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+
| | 2 |
其中正确的是___(把你认为正确结论的序号都填上).

▼优质解答
答案和解析
①如图所示,
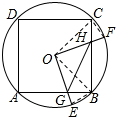
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
在△BOE与△COF中,
,
∴△BOE≌△COF,
∴BE=CF,
∴
=
,①正确;
②∵BE=CF,
∴△BOG≌△COH;
∵∠BOG=∠COH,∠COH+∠OBF=90°,
∴∠GOH=90°,OG=OH,
∴△OGH是等腰直角三角形,②正确.
③如图所示,
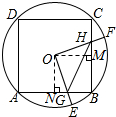
∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③错误;
④∵△BOG≌△COH,
∴BG=CH,
∴BG+BH=BC=4,
设BG=x,则BH=4-x,
则GH=
=
,
∴其最小值为2
,D错误.
故答案为:①②.

∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
在△BOE与△COF中,
|
∴△BOE≌△COF,
∴BE=CF,
∴
 |
| AE |
 |
| BF |
②∵BE=CF,
∴△BOG≌△COH;
∵∠BOG=∠COH,∠COH+∠OBF=90°,
∴∠GOH=90°,OG=OH,
∴△OGH是等腰直角三角形,②正确.
③如图所示,

∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③错误;
④∵△BOG≌△COH,
∴BG=CH,
∴BG+BH=BC=4,
设BG=x,则BH=4-x,
则GH=
| BG2+BH2 |
| x2+(4-x)2 |
∴其最小值为2
| 2 |
故答案为:①②.
看了 如图,边长为4的正方形ABC...的网友还看了以下:
如图四、已知数轴上A、B、C、D四点,对应的实数都是整数,如果A对应的实数为a、B为b、且b-2a 2020-05-15 …
A与B,B与地面的动摩擦因数都是μ,物体AB相对静止,在拉力F的作用下向右做匀加速运动A和B的质量 2020-05-23 …
如图,质量分别为mA、mB的两个弹性小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在 2020-06-12 …
阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣。当A、B两点 2020-06-23 …
(2013•香坊区二模)如图是a、b两种固体物质的溶解度曲线,下列说法正确的是()A.t1℃时,将 2020-07-15 …
如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为"倍角三角形".对于任意的倍角三 2020-07-19 …
如图所示,物体A和B的质量分别为m2和m1,B的水平直角边长为b,A、B之间存在摩擦,B与水平地面 2020-07-21 …
如图,质量分别为mA、mB的两个弹性小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在 2020-07-22 …
正方体物体A和B是同一种材料制成的,它们的边长分别为LA、LB,并且LB=2LA正方体物体A和B是 2020-07-27 …
(9分)如图,质量分别为、的两个小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在B球的 2020-11-01 …