早教吧作业答案频道 -->数学-->
如图,四边形ABCD是O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.(1)求∠OCA的度数;(2)若∠COB=3∠AOB,OC=23,求图中阴影部分面积(结果保留π和根号)
题目详情
如图,四边形ABCD是 O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.
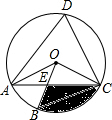
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=2
,求图中阴影部分面积(结果保留π和根号)

(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=2
| 3 |
▼优质解答
答案和解析
(1)∵四边形ABCD是 O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
(2)∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2
,
∴OE=OC•tan∠OCE=2
•tan30°=2
×
=2,
∴S△OEC=
OE•OC=
×2×2
=2
,
∴S扇形OBC=
=3π,
∴S阴影=S扇形OBC-S△OEC=3π-2
.
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
(2)∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2
| 3 |
∴OE=OC•tan∠OCE=2
| 3 |
| 3 |
| ||
| 3 |
∴S△OEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S扇形OBC=
90π×(2
| ||
| 360 |
∴S阴影=S扇形OBC-S△OEC=3π-2
| 3 |
看了 如图,四边形ABCD是O的内...的网友还看了以下:
四边形的四条边分别为a,b,c,d,其中a,c为对边,且满足a平方+b平方+c平方=2ab+2cd 2020-05-15 …
1.下列说法正确的是()A、对角线相等的四边形是平行四边形B、对角线互相垂直的四边形是平行四边形C 2020-06-04 …
四边形四边长顺次为a、b、c、d,且满足a方+b方+c方+d方=2(ab+cd),则这个四边形一点 2020-06-13 …
已知四边形ABCD的四条边长分别为a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2a 2020-07-09 …
已知四边形ABCD的四条边长分别为a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2a 2020-07-09 …
四边形ABCD的四边分别为a、b、c、d,其中a、c为对边,且满足a2+b2+c2+d2=2ab+ 2020-07-30 …
已知四边形ABCD的四条边长分别为a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2ab 2020-10-31 …
已知四边形ABCD的四条边长分别为a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2ab 2020-12-25 …
A,B,I都是XY2型化合物,且阳离子相同A,B阴阳离子之比为1比1,I阴阳离子之比为2比1,且I为 2021-01-18 …
离子方程式中的电荷守恒是左右等号(可逆号)两边阳离子数相等,还是阴离子数相等,还是一边要一边要阴离子 2021-01-18 …