早教吧作业答案频道 -->数学-->
如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.(1)求证:BA•BM=BC•BN;(2)如果CM是O的切线,且M为AB的中点,当BN=4时,求MN的长.
题目详情
如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.
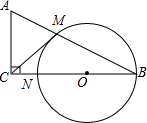
(1)求证:BA•BM=BC•BN;
(2)如果CM是 O的切线,且M为AB的中点,当BN=4时,求MN的长.

(1)求证:BA•BM=BC•BN;
(2)如果CM是 O的切线,且M为AB的中点,当BN=4时,求MN的长.
▼优质解答
答案和解析
(1)证明:如图1,连接MN,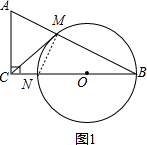
∵NB是 O的直径,
∴∠NMB=90°,
在△ABC和△NBM中,
,
∴△ABC∽△NBM,
∴
=
,
∴BA•BM=BC•BN;
(2)如图2,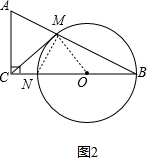 连接MO、MN,
连接MO、MN,
∵∠ACB=90°,M为AB的中点,
∴MC=MB,
∴∠MCB=∠B,
∵CM是 O的切线,
∴∠NMC=∠B,
∵∠MNB=∠NCM+∠NMC,
∴∠MNB=2∠B,
∵BN为 O的直径,
∴∠NMB=90°,
∴∠MNO=60°,
∴△MNO是等边三角形,
∴MN=2.

∵NB是 O的直径,
∴∠NMB=90°,
在△ABC和△NBM中,
|
∴△ABC∽△NBM,
∴
| BA |
| BN |
| BC |
| BM |
∴BA•BM=BC•BN;
(2)如图2,
 连接MO、MN,
连接MO、MN,∵∠ACB=90°,M为AB的中点,
∴MC=MB,
∴∠MCB=∠B,
∵CM是 O的切线,
∴∠NMC=∠B,
∵∠MNB=∠NCM+∠NMC,
∴∠MNB=2∠B,
∵BN为 O的直径,
∴∠NMB=90°,
∴∠MNO=60°,
∴△MNO是等边三角形,
∴MN=2.
看了 如图:在△ABC中,∠ACB...的网友还看了以下:
二次根式的运算已知长方形的长和宽分别为a和b,面积为s(1)当a=3√6,b=4√2时,求S(2)当 2020-03-30 …
已知|a|=4,|b|=5,求下列a与b的数量积(1)a//b;当a//b时,有细塔(就是一个O中 2020-05-14 …
已知函数y=f(x)是定义在R上的奇函数,当x>=0时,f(x)=x+x^21.求x<0时,f(x 2020-05-14 …
已知向量a=(sinx,3/2),b=(cosx,-1),当a//b时,求2(cosx)^2-2s 2020-05-16 …
当东经115°的地方时为9时30分时,东经125°的地方时为多少?科学题,还有一个是A地为东经12 2020-06-12 …
已知a+b=20,求4ab最大值?我现在有两种思路,4a=b求最大值,a=b求最大值,为什么前者是 2020-07-13 …
知a,b和A,用正弦定理求b时结论有:若a为锐角:a 2020-08-02 …
做基本不等式题的时候能不能直接用a=b来求最值啊就是那个当且仅当a=b时“=”成立,等号时就是最做 2020-08-03 …
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x^2-2x(1)求当x<0时,f(x)的解 2020-12-03 …
已知锐角三角形边a与角A求边b和边c可得b=a/A的正切值c=a/正弦值;已知锐角三角形边a与角B求 2020-12-25 …