早教吧作业答案频道 -->数学-->
如图,圆C:x2-(2+a)x+y2-ay+2a=0.(Ⅰ)若圆C与x轴相切,求圆C的方程;(Ⅱ)已知a>2,圆C与x轴相交于两点M,N(点M在点N的左侧).过点M任作一条直线与圆O:x2+y2=10相交于两点A,B.问
题目详情
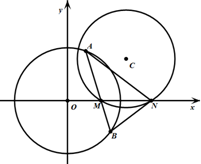
如图,圆C:x2-(2+a)x+y2-ay+2a=0.
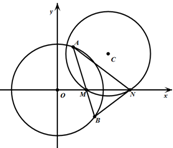
(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知a>2,圆C与x轴相交于两点M,N(点M在点N的左侧).过点M任作一条直线与圆O:x2+y2=10相交于两点A,B.问:是否存在实数a,使得∠ANM=∠BNM?若存在,求出实数a的值,若不存在,请说明理由.

(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知a>2,圆C与x轴相交于两点M,N(点M在点N的左侧).过点M任作一条直线与圆O:x2+y2=10相交于两点A,B.问:是否存在实数a,使得∠ANM=∠BNM?若存在,求出实数a的值,若不存在,请说明理由.
▼优质解答
答案和解析
(Ⅰ)由方程组
可得:x2-(2+a)x+2a=0,
由题意得△=(2+a)2-8a=(a-2)2=0,
所以a=2
故所求圆C的方程为C:x2-4x+y2-2y+4=0.
(Ⅱ)令y=0,得:x2-(2+a)x+2a=0,即(x-2)(x-a)=0.
所以M(2,0),N(a,0)…(5分)
假设存在实数a,
当直线AB与x轴不垂直时,
设直线AB的方程为:y=k(x-2),
代入x2+y2=10得,(1+k2)x2-4k2x+4k2-10=0,
设A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=
.
因为
+
=
而(x1-2)(x2-a)+(x2-2)(x1-a)=2x1x2-(a+2)(x1+x2)+4a=2•
-(a+2)
+4a=
,
因为∠ANM=∠BNM,
所以
+
=0,即
=0,得a=5.
当直线AB与x轴垂直时,也成立.
故存在a=5,使得∠ANM=∠BNM.
|

可得:x2-(2+a)x+2a=0,
由题意得△=(2+a)2-8a=(a-2)2=0,
所以a=2
故所求圆C的方程为C:x2-4x+y2-2y+4=0.
(Ⅱ)令y=0,得:x2-(2+a)x+2a=0,即(x-2)(x-a)=0.
所以M(2,0),N(a,0)…(5分)
假设存在实数a,
当直线AB与x轴不垂直时,
设直线AB的方程为:y=k(x-2),
代入x2+y2=10得,(1+k2)x2-4k2x+4k2-10=0,
设A(x1,y1),B(x2,y2),
则x1+x2=
| 4k2 |
| 1+k2 |
| 4k2-10 |
| 1+k2 |
因为
| y1 |
| x1-a |
| y2 |
| x2-a |
| k[(x1-2)(x2-a)+(x2-2)(x1-a)] |
| (x1-a)(x2-a) |
而(x1-2)(x2-a)+(x2-2)(x1-a)=2x1x2-(a+2)(x1+x2)+4a=2•
| 4k2-10 |
| 1+k2 |
| 4k2 |
| 1+k2 |
| 4a-20 |
| 1+k2 |
因为∠ANM=∠BNM,
所以
| y1 |
| x1-a |
| y2 |
| x2-a |
| 4a-20 |
| 1+k2 |
当直线AB与x轴垂直时,也成立.
故存在a=5,使得∠ANM=∠BNM.
看了 如图,圆C:x2-(2+a)...的网友还看了以下:
如图,直线m、n在平面α内,且m与n相交于点P,试用符号语言写出所有点与线、点与面、线与线、线与面 2020-05-17 …
已知空间三条直线l、m、n.若l与m异面,且l与n异面,则()A.m与n异面B.m与n相交C.m与 2020-07-13 …
1.已知:点P为正方形ABCD的边AD上一点,若AB=6,PA=2,M为BP中点(1)半径为多少时 2020-07-14 …
如图,已知∠AOB=30°,M为OB边上一点,以M为圆心、2cm为半径作M.若⊙M在OB边上运动, 2020-07-24 …
m+n=0n+p=0m-q=0则A.p与q相等B.m与p互为相反数C.m与n相等D.n与q相等 2020-07-30 …
已知:m+n=0,n+p=0,m+q=0,则()A.p与q相等B.m与n互为相反数C.m与n相等D 2020-07-30 …
平面α外有两条直线m和n,如果m和n在平面α内的射影分别是m′和n′,给出下列四个命题:①m′⊥n 2020-07-30 …
平面a外有两条直线m和n,如果m和n在平面a内的射影分别是m1和n1,给出下列四个命题:①m1⊥n 2020-07-30 …
平面α外有两条直线m和n,如果m和n在平面α内的射影分别是m1和n1,给出下列四个命题:①m1⊥n 2020-07-30 …
不正确的命题(1816:26:49)1、平面A外两条直线m和n在平面内A的射影分别为m’和n’,给出 2020-11-14 …