（2014•乌鲁木齐）在平面直角坐标系xOy中，抛物线y=mx2-2x与x轴正半轴交于点A，顶点为B．（1）求点B的坐标（用含m的代数式表示）；（2）已知点C（0，-2），直线AC与BO相交于点D，与该抛物线

Question

（2014•乌鲁木齐）在平面直角坐标系xOy中，抛物线y=mx²-2x与x轴正半轴交于点A，顶点为B．
（1）求点B的坐标（用含m的代数式表示）；
（2）已知点C（0，-2），直线AC与BO相交于点D，与该抛物线对称轴交于点E，且△OCD≌△BED，求m的值；
（3）在由（2）确定的抛物线上有一点N（n，-(5)/(3)），N在对称轴的左侧，点F，G在对称轴上，F在G上方，且FG=1，当四边形ONGF的周长最小时：
①求点F的坐标；
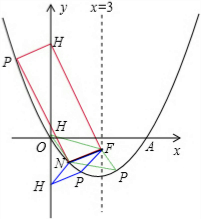
②设点P在抛物线上，在y轴上是否存在点H，使以N，F，H，P为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．

Answer 1

（1）∵y=mx²-2x=m（x-(1)/(m)）²-(1)/(m)，
∴顶点B的坐标为（(1)/(m)，-(1)/(m)）；

（2）∵点C（0，-2），
∴OC=2．
设抛物线的对称轴与x轴交于点M．
∵ME∥y轴，
∴△AME∽△AOC，
∴(ME)/(OC)=(AM)/(AO)=(1)/(2)，
∴ME=(1)/(2)OC=1．
∵△OCD≌△BED，
∴OC=BE=2，
∴BM=BE+ME=3，
∴-(1)/(m)=-3，
∴m=(1)/(3)；

（3）由（2）得抛物线的解析式为y=(1)/(3)x²-2x，其对称轴是直线x=3，A（6，0）．
①∵点N（n，-(5)/(3)）在此抛物线上，
∴-(5)/(3)=(1)/(3)n²-2n，
解得n₁=1，n₂=5．
∵点N在对称轴的左侧，
∴n=1，
∴N（1，-(5)/(3)）．
将点N向上平移1个单位得到N′（1，-(2)/(3)），连结AN′，与对称轴的交点即为所求点F．在对称轴上将点F向下平移1个单位得到点G，连结NG，OF，可知此时得到的四边形ONGF的周长最小（由N′F′+AF′＞AN′，可得NG′+OF′＞NG+OF）．
设直线AN′的解析式为y=kx+b，
把N′（1，-(2)/(3)），A（6，0）代入，
得

k+b＝−(2)/(3)

6k+b＝0

，解得

作业帮用户 2017-10-20

问题解析

（1）利用配方法将一般式化为顶点式，即可求出顶点B的坐标；
（2）设抛物线的对称轴与x轴交于点M．先由ME∥y轴，得出△AME∽△AOC，根据相似三角形对应边的比相等得出(ME)/(OC)=(AM)/(AO)=(1)/(2)，于是ME=(1)/(2)OC=1．再根据△OCD≌△BED，得到OC=BE=2，于是BM=BE+ME=3，即-(1)/(m)=-3，进而求出m的值；
（3）由（2）得抛物线的解析式为y=(1)/(3)x²-2x，其对称轴是x=3，A（6，0）．
①将N（n，-(5)/(3)）代入y=(1)/(3)x²-2x，求出n的值，得到N点坐标．由于四边形ONGF中，边ON与FG为定值，所以当NG+OF最小时，四边形ONGF的周长最小．于是可将点N向上平移1个单位得到N′（1，-(2)/(3)），连结AN′，与对称轴的交点即为所求点F．在对称轴上将点F向下平移1个单位得到点G，连结NG，OF，根据两点之间线段最短可知此时得到的四边形ONGF的周长最小．运用待定系数法求出直线AN′的解析式，将x=3代入，求出y的值，进而得到点F的坐标；
②N（1，-(5)/(3)），F（3，-(2)/(5)），设H（0，y）．分两种情况讨论：
Ⅰ）当NF为平行四边形的边时，
如果NFHP为平行四边形，由点F向左平移3个单位横坐标为0，求得点P的横坐标为1-3=-2，将x=-2代入y=(1)/(3)x²-2x，
求出P点坐标（-2，(16)/(3)），那么N点先向左平移3个单位，再向上平移(16)/(3)-（-(5)/(3)）=7个单位到点P，依此求出H点纵坐标为-(2)/(5)+7=(33)/(5)，进而得到H点坐标为（0，(33)/(5)）；
如果NFPH为平行四边形，同理求出H点坐标为（0，-(59)/(15)）；
Ⅱ）当NF为平行四边形的对角线时，先求出NF的中点坐标，再根据H与P关于这个中点坐标对称，求出H点坐标为（0，(3)/(5)）．

名师点评

本题考点：

二次函数综合题．

考点点评：

本题是二次函数的综合题型，其中涉及到抛物线的顶点坐标求法，相似三角形的判定与性质，全等三角形的性质，轴对称的性质，运用待定系数法求一次函数的解析式，平行四边形的性质等知识，综合性较强，有一定难度．运用数形结合、分类讨论及方程思想是解题的关键．

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议