早教吧作业答案频道 -->数学-->
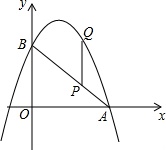
如图,抛物线y=-x2+2x+3分别与x轴正半轴、y轴交于点A,B.点P在线段AB上运动(不与点A,B重合),过点P作P作PQ∥y轴交抛物线于点Q,求PQ的最大值.
题目详情
如图,抛物线y=-x2+2x+3分别与x轴正半轴、y轴交于点A,B.点P在线段AB上运动(不与点A,B重合),过点P作P作PQ∥y轴交抛物线于点Q,求PQ的最大值.

▼优质解答
答案和解析
当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,则A(3,0),
当x=0时,y=-x2+2x+3=3,则B(0,3),
设直线AB的解析式为y=kx+b,
把A(3,0),B(0,3)代入得
,解得
,
所以直线AB的解析式为y=-x+3,
设P(t,-t+3),
而PQ∥y轴,则Q(t,-t2+2t+3),
所以PQ=-t2+2t+3-(-t+3)
=-t2+3t,
当t=-
=
时,PQ最大,最大值=
=
.
当x=0时,y=-x2+2x+3=3,则B(0,3),
设直线AB的解析式为y=kx+b,
把A(3,0),B(0,3)代入得
|
|
所以直线AB的解析式为y=-x+3,
设P(t,-t+3),
而PQ∥y轴,则Q(t,-t2+2t+3),
所以PQ=-t2+2t+3-(-t+3)
=-t2+3t,
当t=-
| 3 |
| 2×(-1) |
| 3 |
| 2 |
| 0-32 |
| 4×(-1) |
| 9 |
| 4 |
看了 如图,抛物线y=-x2+2x...的网友还看了以下:
已知抛物线x^2=y上有一定点A(-1,1)和两个动点Q、P,当PA垂直于PQ时,点Q的横坐标的取 2020-05-13 …
方程x^2/m-1+y^2/m=1表示一个椭圆……设命题P:方程x^2/m-1+y^2/m=1表示 2020-05-16 …
高二抛物线,已知抛物线y^2=x,定点P(t,0)(t>0),定直线l:x=-t,点Q在直线l上, 2020-06-03 …
2道2此函数题目1.已知抛物线y=ax^2+(b-1)x+2若抛物线与直线y=x有两个不同的交点P 2020-06-04 …
已知,抛物线y=-(x-1)^2+4的顶点为A,与x轴相交于B、C两点,直线y=-2x+6经过A、 2020-06-14 …
高二数学圆锥曲线,题挺短的,但是不会已知抛物线C的对称轴为y轴,顶点为A(0,-1)且在x轴上截出 2020-07-11 …
(2013•槐荫区二模)如图,直线y=x与抛物线y=x2-x-3交于A、B两点,点P是抛物线上的一 2020-07-26 …
已知抛物线C:x^2-2py(p>0)的准线被圆x^2+y^2=p^2截得弦长为2根号3,过抛物线 2020-07-26 …
如图,直线y=x与抛物线y=x2-x-3交于A、B两点,点P是抛物线上的一个动点,过点P作直线PQ 2020-07-29 …
如图所示,直线y=x与抛物线y=x2-x-3交于A,B两点,点P是抛物线上的一个动点,点P作PQ⊥ 2020-08-01 …