早教吧作业答案频道 -->数学-->
抛物线y=ax2+c与x轴交于A,B两点,顶点C,点P为抛物线上一点,且位于x轴下方.(1)如图1,若P(1,-3),B(4,0).D是抛物线上一点,满足∠DPO=∠POB,且D与B分布位于直线OP的两侧,求点C
题目详情
抛物线y=ax2+c与x轴交于A,B两点,顶点C,点P为抛物线上一点,且位于x轴下方.
(1)如图1,若P(1,-3),B(4,0).D是抛物线上一点,满足∠DPO=∠POB,且D与B分布位于直线OP的两侧,求点C与点D的坐标;
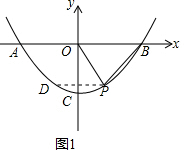
(2)如图2,A,B是抛物线y=ax2+c与x轴的两个交点,直线PA,PB与y轴分别交于E,F两点,当点P在x轴下方的抛物线上运动时,
是否为定值?若是,试求出该定值;若不是,请说明理由(记OA=OB=t)
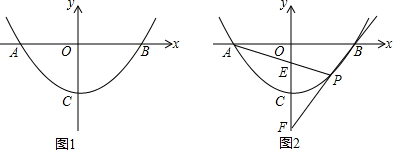
(1)如图1,若P(1,-3),B(4,0).D是抛物线上一点,满足∠DPO=∠POB,且D与B分布位于直线OP的两侧,求点C与点D的坐标;
(2)如图2,A,B是抛物线y=ax2+c与x轴的两个交点,直线PA,PB与y轴分别交于E,F两点,当点P在x轴下方的抛物线上运动时,
| OE+OF |
| OC |

▼优质解答
答案和解析
 (1)将P(1,-3),B(4,0)代入y=ax2+c,得
(1)将P(1,-3),B(4,0)代入y=ax2+c,得
,
解得
,
抛物线的解析式为y=
x2-
.
∴C(0,-
)
如图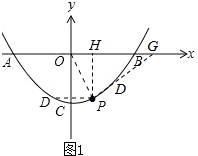 1,
1,
当点D在OP左侧时,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,-3),
得D(-1,-3);
(2)点P运动时,
是定值,定值为2,理由如下: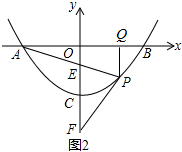
作PQ⊥AB于Q点,设P(m,am2+c),A(-t,0),B(t,0),则at2+c=0,c=-at2.
∵PQ∥OF,
∴
=
,
∴OF=
=-
=
=amt+at2.
同理OE=-amt+at2.
∴OE+OF=2at2=-2c=2OC.
∴
=2.
 (1)将P(1,-3),B(4,0)代入y=ax2+c,得
(1)将P(1,-3),B(4,0)代入y=ax2+c,得
|
解得
|
抛物线的解析式为y=
| 1 |
| 5 |
| 16 |
| 5 |
∴C(0,-
| 16 |
| 5 |
如图
 1,
1,当点D在OP左侧时,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,-3),
得D(-1,-3);
(2)点P运动时,
| OE+OF |
| OC |

作PQ⊥AB于Q点,设P(m,am2+c),A(-t,0),B(t,0),则at2+c=0,c=-at2.
∵PQ∥OF,
∴
| PQ |
| OF |
| BQ |
| BO |
∴OF=
| PQ•BO |
| BQ |
| -(am2+c)t |
| t-m |
| (am2-at2)t |
| m-t |
同理OE=-amt+at2.
∴OE+OF=2at2=-2c=2OC.
∴
| OE+OF |
| OC |
看了 抛物线y=ax2+c与x轴交...的网友还看了以下:
以下判断正确的是()A.只有在点燃或加热时可燃物才能燃烧B.只要使可燃物的温度降到着火点以下就能灭 2020-05-12 …
下列哪些情况下的物体可以看成是质点()A.从北京开往上海的一列火车B.跳芭蕾舞的演员C.形状不规则 2020-05-14 …
已知;抛物线Y=ax^2+2x+c,对称轴位直线x=-1,抛物线与y轴交与点c抛物线与Y轴交于点C 2020-05-16 …
化学关于沸点下列物质中有固定沸点的是A.食用醋 B.油酸甘油酯 C.豆油 D.黄油为什么?它的成分 2020-05-17 …
平行四边形ABCD中,AB=4,D点坐标为(0,8),以点C为顶点的抛物线y=ax²+bx+c经过 2020-05-23 …
前照灯的近光灯丝位于()A.焦点上方B.焦点上C.焦点下D.焦点正中 2020-05-31 …
前照灯的远光灯丝位于()A.焦点上方B.焦点上C.焦点下D.焦点正中 2020-05-31 …
如图已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0, 2020-06-14 …
将抛物线y=x2-4x+4沿y轴向下平移9个单位,所得新抛物线与x轴正半轴交于点B,与y轴交于点C 2020-06-23 …
金属的熔点排列1.下列物质中,熔点最高的是()A.纯铁B.铁合金C.黄铜D.铝合金2.下列物质中, 2020-07-06 …