早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系xOy中,直线y=12x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)直接写出点B的坐标;(2)求抛物线解
题目详情
如图,在平面直角坐标系xOy中,直线y=
x+2与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-
且经过A、C两点,与x轴的另一交点为点B.
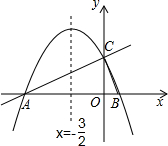
(1)直接写出点B的坐标;
(2)求抛物线解析式.
(3)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
| 1 |
| 2 |
| 3 |
| 2 |
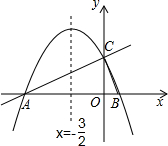
(1)直接写出点B的坐标;
(2)求抛物线解析式.
(3)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
▼优质解答
答案和解析
(1)①y=
当x=0时,y=2,当y=0时,x=-4,
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于x=-
对称,
∴点B的坐标为1,0).
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a
∴a=-
∴y=-
x2-
x+2.
(2)设P(m,-
m2-
m+2).
过点P作PQ⊥x轴交AC于点Q,
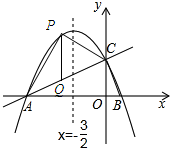
∴Q(m,
m+2),
∴PQ=-
m2-
m+2-(
m+2)
=-
m2-2m,
∵S△PAC=
×PQ×4,
=2PQ=-m2-4m=-(m+2)2+4,
∴当m=-2时,△PAC的面积有最大值是4,
此时P(-2,3).
| 1 |
| 2 |
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于x=-
| 3 |
| 2 |
∴点B的坐标为1,0).
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a
∴a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)设P(m,-
| 1 |
| 2 |
| 3 |
| 2 |
过点P作PQ⊥x轴交AC于点Q,

∴Q(m,
| 1 |
| 2 |
∴PQ=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
∵S△PAC=
| 1 |
| 2 |
=2PQ=-m2-4m=-(m+2)2+4,
∴当m=-2时,△PAC的面积有最大值是4,
此时P(-2,3).
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
高一物理题抛体问题斜面与水平面成37度角,现从斜面上正以10m/s垂直于斜面抛出一个物体,求:1〉 2020-06-02 …
高一物理——抛体运动:竖直上抛把一个小球以30m/s的速度从地面竖直上抛出.隔一秒时间,再从同一处 2020-06-05 …
在竖直杆上安装一个光滑小导向槽,使竖直上抛的小球能改变方向后做平抛运动,不计经导向槽时的能量损失, 2020-06-24 …
某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.(1)以隧道横断面抛物线的顶点为原点,以抛物线 2020-07-05 …
某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.(1)以隧道横断面抛物线的顶点为原点,以抛物线 2020-07-05 …
已知:抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧),顶点为P.(1)求A、 2020-07-26 …
下列现象中不属于利用惯性的是()A.通过拍打窗帘清除它上面的浮灰B.用力将物体抛出去,物体最终要落 2020-08-01 …
(2006•盐城)已知:抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧),顶点为 2020-11-12 …
(2006•盐城)已知:抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧),顶点为 2020-11-12 …
如图,O点是小球平抛运动抛出点;在O点有一频闪点光源,闪光频率为30Hz;在抛出点的正前方,竖直放置 2020-11-25 …