求证:(1)若射影定理成立则勾股定理成立;(2)若勾股定理成立则射影定理成立.

Question

求证:(1)若射影定理成立 则勾股定理成立;

(2)若勾股定理成立 则射影定理成立.

Answer 1

图 1-5-16

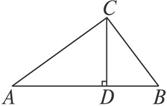
证明:如图 Rt△ABC中 CD为斜边上的高.

(1)由射影定理AC ² =AD·AB BC ² =BD·AB

∴AC ² +BC ² =AD·AB+BD·AB

=(AD+BD)·AB

=AB ²

即勾股定理成立.

(2)∵AB=AD+BD

∴AB ² =(AD+BD) ² =AD ² +BD ² +2AD·BD.

∴AB ² -AD ² -BD ² =2AD·BD.

∴AC ² +BC ² -AD ² -BD ² =2AD·BD.

∴(AC ² -AD ² )+(BC ² -BD ² )=2AD·BD.

∴CD ² +CD ² =2AD·BD.

∴CD ² =AD·BD.①

∵AC ² =CD ² +AD ²

=AD·BD+AD ²

=AD(BD+AD)

=AD·AB ②

同理 BC ² =BD·AB.③

由①②③说明若勾股定理成立 则射影定理成立.