早教吧作业答案频道 -->数学-->
在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”.拓展到空间(如图),类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的结论
题目详情
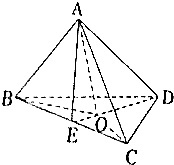
在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”.拓展到空间(如图),类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的结论是___.

▼优质解答
答案和解析
由边对应着面,
边长对应着面积,
由类比可得:三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△ABC2+S△ACD2+S△ADB2,
故答案为:设三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△BCD2 =S△ABC2+S△ACD2+S△ADB2.
边长对应着面积,
由类比可得:三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△ABC2+S△ACD2+S△ADB2,
故答案为:设三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△BCD2 =S△ABC2+S△ACD2+S△ADB2.
看了 在平面几何里,有勾股定理:“...的网友还看了以下:
已知三棱台ABC-A'B'C'中,SΔABC=9,SΔA'B'C'=4,高h=3求三棱锥A'-ABC 2020-03-30 …
圆柱的体积大于和它等底等高圆锥的体积?这句话对吗?请说明基本原理及其公式好吗谢谢(1)一个圆锥体, 2020-04-11 …
若正棱锥的底面边长和侧棱长相等,则该棱锥一定不是()A.正三棱锥B.正四棱锥C.正五棱锥D.正六棱 2020-04-24 …
12.在正三棱锥中,有一半球,其底面与正三棱锥的底面重合,正三棱锥的三个侧面都和半球相切.如果半球 2020-04-24 …
在正三棱锥内有一半球,其底面与正三棱锥的底面在同一平面内,正三棱锥的三个侧面都和半球相切.如果半球 2020-04-24 …
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.已知同底的两个正三棱锥内接于同一个球.已 2020-04-24 …
以三棱锥各面重心为顶点得到一个新三棱锥,则它的表面积是原三棱锥表面积的A.1/16B.1/9C.1 2020-05-13 …
已知四棱锥P-ABCD中,底面ABCD为正方形,边长为a,PB=3a,PD=a,PA=PC=2a, 2020-05-14 …
问道物理中考题,谢谢【【【【【【】】】】】】】29.(4分)在综合实践活动中,某兴趣小组的同学利用 2020-05-17 …
理财目标方程式右边相当于(),左边相当于以现有资产和未来年储蓄能力计算的()A.理财目标的总需求 2020-05-22 …