早教吧作业答案频道 -->数学-->
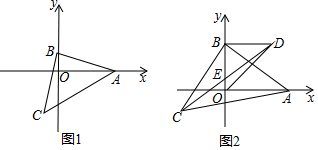
已知:点A(4,0),点B是y轴正半轴上一点,如图1,以AB为直角边作等腰直角三角形ABC.(1)当点B坐标为(0,1)时,求点C的坐标;(2)如图2,以OB为直角边作等腰直角△OBD,点D在第一象
题目详情
已知:点A(4,0),点B是y轴正半轴上一点,如图1,以AB为直角边作等腰直角三角形ABC.
(1)当点B坐标为(0,1)时,求点C的坐标;
(2)如图2,以OB为直角边作等腰直角△OBD,点D在第一象限,连接CD交y轴于点E.在点B运动的过程中,BE的长是否发生变化?若不变,求出BE的长;若变化,请说明理由.
(1)当点B坐标为(0,1)时,求点C的坐标;
(2)如图2,以OB为直角边作等腰直角△OBD,点D在第一象限,连接CD交y轴于点E.在点B运动的过程中,BE的长是否发生变化?若不变,求出BE的长;若变化,请说明理由.

▼优质解答
答案和解析
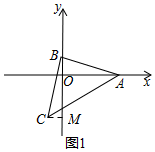 (1)如图1,过C作CM⊥y轴于M.
(1)如图1,过C作CM⊥y轴于M.
∵CM⊥y轴,
∴∠BMC=∠AOB=90°,
∴∠ABO+∠BAO=90°
∵∠ABC=90°,
∴∠CBM+∠ABO=90°,
∴∠CBM=∠BAO,
在△BCM与△ABO中,
,
∴△BCM≌△ABO(AAS),
∴CM=BO=1,BM=AO=4,
∴OM=3,
∴C(-1,-3);
(2)在B点运动过程中,BE长保持不变,BE的长为2,
理由:如图2,过C作CM⊥y轴于M,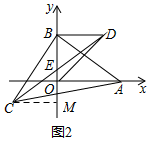
由(1)可知:△BCM≌△ABO,
∴CM=BO,BM=OA=4.
∵△BDO是等腰直角三角形,
∴BO=BD,∠DBO=90°,
∴CM=BD,∠DBE=∠CME=90°,
在△DBE与△CME中,
,
∴△DBE≌△CME(AAS),
∴BE=EM,
∴BE=
BM=2.
 (1)如图1,过C作CM⊥y轴于M.
(1)如图1,过C作CM⊥y轴于M.∵CM⊥y轴,
∴∠BMC=∠AOB=90°,
∴∠ABO+∠BAO=90°
∵∠ABC=90°,
∴∠CBM+∠ABO=90°,
∴∠CBM=∠BAO,
在△BCM与△ABO中,
|
∴△BCM≌△ABO(AAS),
∴CM=BO=1,BM=AO=4,
∴OM=3,
∴C(-1,-3);
(2)在B点运动过程中,BE长保持不变,BE的长为2,
理由:如图2,过C作CM⊥y轴于M,

由(1)可知:△BCM≌△ABO,
∴CM=BO,BM=OA=4.
∵△BDO是等腰直角三角形,
∴BO=BD,∠DBO=90°,
∴CM=BD,∠DBE=∠CME=90°,
在△DBE与△CME中,
|
∴△DBE≌△CME(AAS),
∴BE=EM,
∴BE=
| 1 |
| 2 |
看了 已知:点A(4,0),点B是...的网友还看了以下:
如图,在平面直角坐标系中,O为坐标原点,三角形OAB为等边三角形,点A的坐标是(4倍根3,0),点 2020-04-27 …
直角坐标系中A(4,2)O为坐标原点,在x轴上另有一点B,如果以O,A,B为顶点的三角形是等腰三角 2020-05-16 …
在平面直角坐标系内,点0为坐标原点,点A,B的坐标分别为(x,y),(x+6,y)~在平面直角坐标 2020-06-02 …
已知,如图,在角MON的边OM和ON上有两点A,B角MAB与角NBA的平分线交与点C(1)求证:点 2020-06-13 …
已知一个边长为2的正方形OABC在平面直角坐标系中,点O为坐标原点,B,C两点在第二象限内,OA与 2020-07-30 …
正比例函数y=kx(k不等于0)的图像与反比例函数y=-2/x的图像相交于A,B两点,其中点B的纵 2020-07-30 …
如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限 2020-07-30 …
已知:等腰梯形OAB在直角坐标系中的位置如图.OA=OB,点A的坐标为(-1,-根号3),点B的坐 2020-08-01 …
在平面直角坐标系内y=3\4x+3与两坐标轴交于A、B两点,点O为坐标原点,若在该坐标平面内有以点P 2020-11-03 …
已知,等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(-3根号3,3)点B的坐标为(6,0) 2020-12-21 …