一块材料的形状是锐角三角形ABC，边BC=120mm，高AD=80mm，把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．（1）求证：△AEF∽△ABC；（2）求这个正方形零件

Question

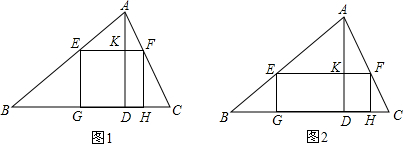
一块材料的形状是锐角三角形ABC，边BC=120mm，高AD=80mm，把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．
（1）求证：△AEF∽△ABC；
（2）求这个正方形零件的边长；
（3）如果把它加工成矩形零件如图2，问这个矩形的最大面积是多少？

Answer 1

（1）∵四边形EGFH为矩形，
∴BC∥EF，
∴△AEF∽△ABC；
（2）设正方形零件的边长为a
在正方形EFGH中，EF∥BC，EG∥AD
∴△AEF∽△ABC，△BEG∽△BAD
∴(EF)/(BC)=(AE)/(AB)，(EG)/(AD)=(BE)/(AB)，
∴(EF)/(BC)+(EG)/(AD)=(AE)/(AB)+(BE)/(AB)=1，
即：(a)/(120)+(a)/(80)=1
解得：a=48
即：正方形零件的边长为48；
（3）设长方形的长为x，宽为y，
当长方形的长在BC时，
由（1）知：(y)/(120)+(x)/(80)=1，
∵(y)/(120)+(x)/(80)≥2√((y)/(120)×(x)/(80))，
∴当(y)/(120)=(x)/(80)=0.5，即x=60，y=40，xy最大为2400
当长方形的宽在BC时，(x)/(120)+(y)/(80)=1，
∵(x)/(120)+(y)/(80)≥2√((x)/(120)×(y)/(80))，
∴当(x)/(120)=(y)/(80)=0.5，即x=40，y=60，xy最大为2400，
又∵x≥y，所以长方形的宽在BC时，面积<2400
综上，长方形的面积最大为2400．